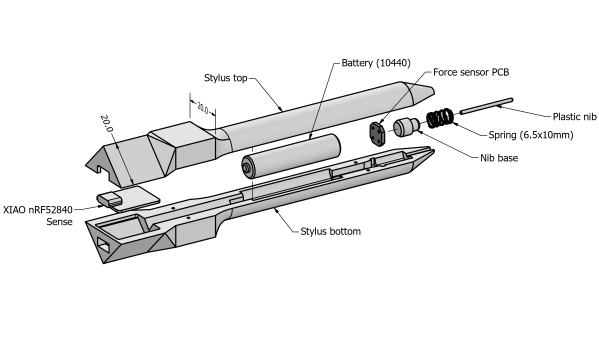
[Jcparkyn] clearly had an interesting topic for their thesis project, and was conscientious enough to write up a chunk of it and release it to the wild. The project in question is a digital pen that uses some neat sensor fusion to combine the inputs from a pen-mounted gyro/accelerometer with data from an optical tracking system provided by an off-the-shelf webcam.
A six degrees of freedom (6DOF) tracking system is achieved as a result, with the pen-mounted hardware tracking orientation and the webcam tracking the 3D position. The pen itself is quite neat, with an ALPS/Alpine HSFPAR003A load sensor measuring the contact pressure transmitted to it from the stylus tip. A Seeed Xaio nRF52840 sense is on duty for Bluetooth and hosting the needed IMU. This handy little module deals with all the details needed for such a high-integration project and even manages the charging of a single 10440 lithium cell via a USB-C connector.
Positional tracking uses Visual Pose Estimation (VPE) assisted with ArUco markers mounted on the end of the stylus. A consumer-grade (i.e. uncalibrated) webcam is all that is required on the hardware side. The software utilizes the familiar OpenCV stack to unroll the effects of the webcam rolling shutter, followed by Perspective-n-Point (PnP) to estimate the pose from the corrected image stream. Finally, a coordinate space conversion is performed to determine the stylus tip position relative to the drawing surface.
stylus. A consumer-grade (i.e. uncalibrated) webcam is all that is required on the hardware side. The software utilizes the familiar OpenCV stack to unroll the effects of the webcam rolling shutter, followed by Perspective-n-Point (PnP) to estimate the pose from the corrected image stream. Finally, a coordinate space conversion is performed to determine the stylus tip position relative to the drawing surface.
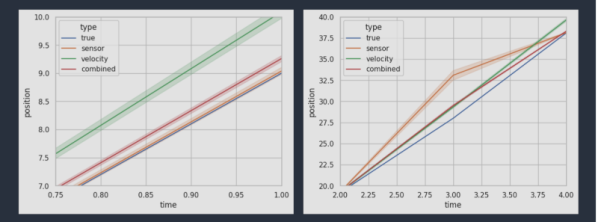
The sensor fusion is taken care of with a Kalman filter, smoothed with the typical Rauch-Tung-Striebel (RTS) algorithm before being passed onto the final application. This process is running in Python using the NumPy module, as you would expect, but accelerated using the Numba JIT compiler.
Motion tracking is not news to us, we’ve seen many an implementation over the years, such as this one. But digital input pens? Why aren’t they more of a thing?
Thanks to [Oliver] for the tip!