Instructables user [Osprey22] has been building towards this Christmas for years. Why? This year, he has brought an impressive musical Christmas light display inside, and at a fraction of the cost too!
An box at the tree’s base hides the power supply and the controller boards — a Raspberry Pi and a SanDevices e682 Pixel controller for the 400 WS2811 RGB LEDs — with an added router to connect them to the main network. The Pi is running Falcon Pi Player and a projector somewhere in the region of $100 complements the light show.
As far as mapping out the LEDs, Xlights is the program of choice, locating the LEDs in space with the help of a cell phone video recording. [Osprey22] had to write a quick program in C to fix the LED overlaps in the grid. (A spreadsheet would work just as well, here). Oh, and the gifts at the bottom of the tree double as a projector screen!
The result is one of the most impressive Christmas trees we’ve seen — and there is some stiff competition out there.

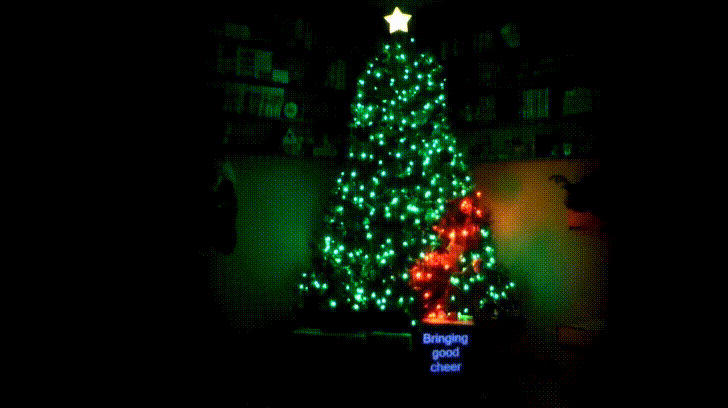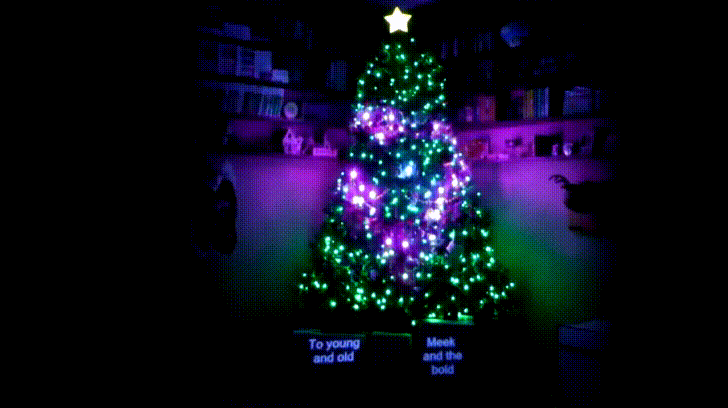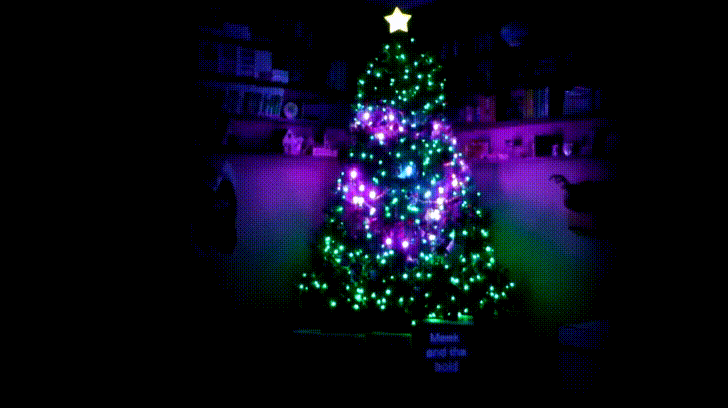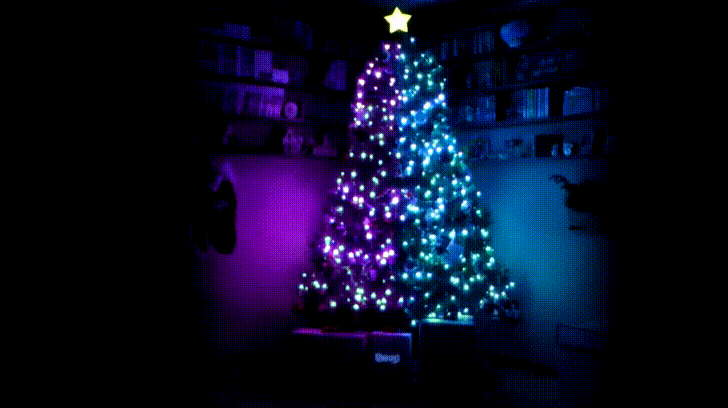














Not sure how Moana is connected to Christmas, but even those parts were pretty bad ass! Cool project!!
Moana is the Hook for the kids…… sorry :P
@Jake: Mele Kalikimaka!
drat copyright takedown
Very impressive. And I’ve been wondering about mapping pixels to physical location. Sounds like he figured that out. A video on his cell phone and then CV to create the map. Anyone know if there is any application that will do that? I don’t think Xlights does that part.
I’d be interested too. Something like JunkyardJumbotron but for neopixels.
xlights does have a feature in it to help map leds, under tools -> “generate customer model”( something new this year)
What is the best strategy for powering a long run of these LEDs?
If you just power them from one end presumably the other end will be dimmer right?
yes, to solve that issue = power injection…. depending on the voltage of the LEDs, 5 volt leds = every 50 for power injection and 12 volt leds = every 100 leds. thought i’m push 125 on one of my strings.
On an ordinary 12V string 300 (60LEDs/m, 5m) are quite OK.
yes, to solve that issue = power injection…. depending on the voltage of the LEDs, 5 volt leds = every 50 for power injection and 12 volt leds = every 100 leds. thought i’m push 125 on one of my strings.
Looks spectacular
I had a similar idea for my tree. I’m going to take a risk and share this link: https://www.treecam.net/ I’m not sure my server will handle much traffic!
I’ve been playing with your christmas tree for a while now.
Thanks for sharing.
Wow a Christmas tree on Steriods. Looks Fab. Must do this next year if I remember.