Space elevators belong to that class of technology that we all want to see become a reality within our lifetimes, but deep-down doubt we’ll ever get to witness firsthand. Like cold fusion, or faster than light travel, we understand the principles that should make these concepts possible, but they’re so far beyond our technical understanding that they might as well be fantasy.
 Except, maybe not. When Japan Aerospace Exploration Agency (JAXA) launches their seventh Kounotori H-II Transfer Vehicle towards the International Space Station, riding along with the experiments and supplies for the astronauts, will be a very special pair of CubeSats. They make up the world’s first practical test of space elevator technology, and with any luck, will be one of many small steps that precedes the giant leap which access to space at a fraction of the cost will be.
Except, maybe not. When Japan Aerospace Exploration Agency (JAXA) launches their seventh Kounotori H-II Transfer Vehicle towards the International Space Station, riding along with the experiments and supplies for the astronauts, will be a very special pair of CubeSats. They make up the world’s first practical test of space elevator technology, and with any luck, will be one of many small steps that precedes the giant leap which access to space at a fraction of the cost will be.
Of course, they won’t be testing a fully functional space elevator; even the most aggressive of timelines put us a few decades out from that. This will simply be a small scale test of some of the concepts that are central to building a space elevator, as we need to learn to crawl before we can walk. But even if we aren’t around to see the first practical space elevator make it to the top, at least we can say we were there on the ground floor.
Going Up. Way, Way Up
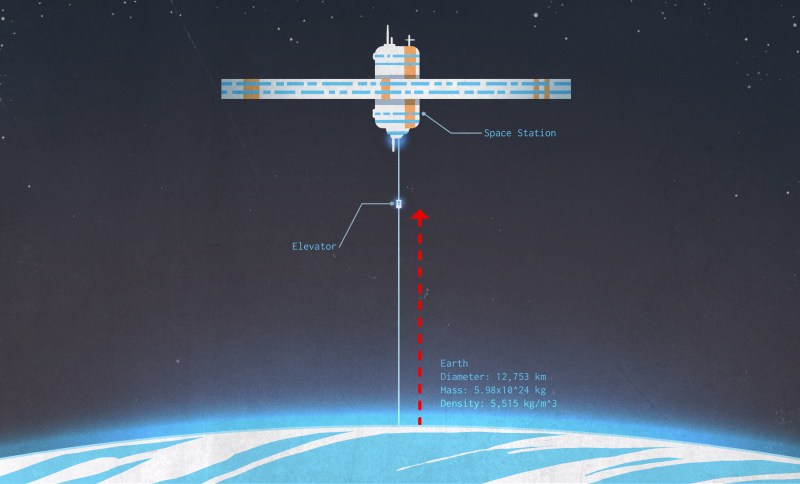
In a fully realized space elevator, an incredibly strong cable would attach an orbital platform to the surface of the Earth. Electrically powered vehicles (usually referred to as “climbers”) would ride this cable from the ground, through the atmosphere, and directly into space. No rocket engines, no G forces pinning you to the seat. No flying at all, really. Just a smooth vertical ride at a leisurely pace of 200 hundred kilometers per hour or so. Physically it would be an easy trip, free from the rigors of a traditional space launch. But it certainly wouldn’t be a quick one.
For the space elevator to work, the “top floor” needs to be in what’s called a geostationary orbit. This means that the platform’s orbital period would match Earth’s rotational period, giving the appearance (from our perspective on the surface) that it’s hovering motionless above us. This is the same orbit that many communications satellites are placed in, as it negates the need to actively track them across the sky. The problem is, geostationary orbit around Earth is at an altitude of 36,000 km (22,370 miles). At 200 km/h, it would take over a week for a climber to reach that altitude.
A Tall Order
As you can imagine, given its size and complexity, building a space elevator would be extremely expensive: the Obayashi Corporation, a Japanese firm that hopes to build a space elevator by the year 2050, estimates it will cost approximately $90 billion USD. But a space elevator is a piece of infrastructure, like a highway or rail line. It costs a lot of money up front, but it enables cheaper travel in the long run. With regular “climbs”, it’s estimated an elevator could bring the cost of putting a payload into space down to $220 per kilogram ($100 per pound). That’s less than 1/10th of what it costs to fly on the already very cheap Falcon 9 rocket.
So it’s not terribly fast, and it costs a lot of money to build, but it overall still sounds like a good investment for any civilization that’s hoping to get off the rock they evolved on. So why haven’t we built one? The simple answer is, we don’t know how.
While the principle seems simple enough, the material science still eludes us. Building a rocket that can make it to space (and occasionally back, depending on who built it) is already pushing our metallurgic capabilities to the limit. But a cable that could stretch 36,000 km without breaking is beyond our current level of technology. Carbon nanotubes hold the most promise, but we aren’t yet proficient enough in manufacturing with them.
Testing Our Mettle with a First Climb
The upcoming test will use two 1U CubeSats (each measuring 10 cm per side) deployed from the International Space Station to stand in as the Earth and orbital platform. The two CubeSats will be ejected from the ISS as one unit, but will then separate and move away from each other. They’ll be linked together by a 10 meter (~33 foot) long steel tether, and then if everything goes according to plan, a tiny motorized climber will attempt to move from one satellite to the other.

Measuring just 6x3x3cm, the miniature climber will be the first object in history to attempt such a maneuver. Theoretically we have a pretty good understanding of what will happen when the diminutive rider starts pulling on the cable, but theory and assumptions don’t always play nice in space. Cameras on the satellites will monitor the climber as it goes, and a wealth of invaluable real-world data will be collected to help refine engineer’s plans for larger scale tests in the future.
This mission builds on the success of previous Space Tethered Autonomous Robotic Satellite (STARS) missions launched by JAXA in 2009, 2004, and 2016. These missions tested the deployment and stability of the tether, which was also a first. After gaining an understanding on how the tethered vehicles alone behaved, the team behind the STARS missions at Shizuoka University now feel confident enough to move onto the next phase.
Ambition of a Century
First conceived in 1895 by Russian scientist Konstantin Tsiolkovsky, and popularized in the 20th century by the works of science fiction luminaries such as Arthur C. Clarke and Robert A. Heinlein, space elevators are second to perhaps only warp drive in terms of “Holy Grail” space technologies. Its been argued that, once humanity has a functional space elevator, we’ll be well on the way to colonizing the solar system.
Our attempts at realizing the technology thus far have been limited in scope, but we may finally be seeing the first glimpses of light at the end of the tunnel. We’ve still got a few decades to go, so there’s still plenty to be gained from coming up with alternate ways into space. But there’s also no question that we’re now closer than ever to obsoleting rocket technology that’s been almost unchanged since its development during World War II.
















One of the best parts about a space elevator is that you cannot hear the Muzak.
Yes, a direct corollary to not hearing a scream in space!
There was a cartoon in Stereo Review decades ago, it showed several people holding down a struggling bearded man outside an elevator. A bystander is being told; “He just heard his ‘Death to the Fascist Pigs!’ on the elevator Muzak!”
The proper corollary would be to compare the inside of the elevator car to the inside of space craft. Would you really travel that ar for any length of time with nothing to breath?
Satire intent not indicated. You will hear any Muzak provided for our listening pleasure’; for humans to survive inside there has to be an artificial pressurized atmosphere. Astronauts are able to speak to each other and ground control?
Is this better?
One of the best parts about a space elevator is that you cannot hear the Muzak.
That was a joke. son. I say a joke.
Obligatory reference to Foghorn Leghorn.
AS long as it was obligatory, why wasn’t it to Kenny Delmar?
At a 10 meter distance, I suspect the “climbing” cubesat will just pull the two closer together.
Depends — if the two cubesats are rotating around each other sufficiently quickly, their centripetal forces will prevent the climber (not a cubesat) from drawing them together. Since a real elevator would have lots of tension in its cable, I’d expect this test to emulate that with such rotation.
It wont work because halfway up the weight of the construction gets to heavy and gets pulled down by earth gravitation.
And the Earth’s crust is only 25 miles thick, anything really big or heavy will punch through to the magma.
If you build it tall enough, the centrifugal force of the earth spinning will pull it up.
Exactly this, you have to remember that a space elevator isn’t resting on the Earth, it’s in geosynchronous orbit.
Actually, the top of the elevator will likely have to be further out than geostationary orbit, to provide a counterweight. And it will still need some positioning thrusters for minor adjustments
My vision for a space elevator is something like scaffolding that is like a hover craft that Swageloks or connects somehow easily as each unit hovers into place where fuel or power is transferred using the scaffold pipes themselves so that the hover prime movers (chemical rockets, duct fans or gas turbines maybe) can then be real time positioned so to balance and load equalize the system as the length grows where maybe some of the higher level units will need to be air dropped to hover to the top if not rocket guided. I’m thinking the system won’t be able to be electric powered higher up and will need a chemical rocket system to control the positioning and load equilibrium (tension, torsion, etc.). I don’t see how else the system can be controlled since plasma thrusters aren’t powerful enough from my understanding though maybe an all electric system can be devised.
This is definitely one of the greatest material science milestone projects outside of deep underground high temperature insulating systems that can power themselves and cool themselves in I’d say a Venus environment while somehow providing life support in the self sustained system. Maybe magma pool power stations for starters. Then figure out the bombing protocol to clean Venus up since seems there can be some sort of “clean” nuclear reaction or bombing method if though out in detail. Not sure how yet, though seems like more mass to harvest materials from and volume to utilize if not just hovering in the higher level atmosphere that isn’t as dangerous. Again, a maybe even thermonuclear hover craft area of opportunity for a somewhat perpetual maintaining designed hover station with maybe redundant prime movers to to change out one routinely or more safely during a failure.
I don’t think this is true. Objects closer to Earth than the geosynchronous orbit, traveling at Earth-synchronous speed fall back to Earth. If this wasn’t the case, then objects on the Earth’s surface would fly off of it. It’s only when you get to a geosynchronous orbit that the imaginary thing we call centrifugal force equals the gravitational force. This is why satellites stay there. Sure, if you go beyond geosynchronous orbit, then you get pulled up. This is why the proposals for a space elevator go beyond that orbit – to keep it from falling down.
The same applies to the “climber”: while it’s below synchronous orbit, but still at geostationary angular speed, the balance of forces is still toward the Earth. You don’t start getting pulled away from Earth until you get beyond the geostationary orbit.
Apologies if this was meant to be a joke.
That’s why the whole space elevator is in geosynchronous orbit. Mr Brandano responded to my comment above saying ‘actually blah blah’, but missing that being in orbit means having your centre of mass as that orbit, so yes of course there needs to be some mass beyond geosynchronous orbit. One of the ideas is that the end of the tether beyond the orbit could be used to launch vehicles into the solar system.
Like cables at sea: if the upward force of the cable nears its weight, the cable ‘floats’. Hence kevlar is an easier material than steel when working in water; the cable itself doesn’t “add weight” there.
Provisions could be made for the part of the tether that resides in the atmosphere, so as to make it float in air and saving considerably on the wind forces cables have to withstand. Side effect (pun intended) is the uprighting of the lower part of the tether because the ‘float force’ of the atmospheric part of the cable will be perpendicular to the earth’s surface.
Assuming the cable is fully suspended from its outward end, the smallest force is on the near-surface part of the cable. A cone-shaped cable, with the wider end far out, would be logical. Thoughts?
I haven’t got past the thought of “WTF happens when it breaks?”. I’d assume that most of the cable outside the atmosphere would burn upon reentry, so that would just leave about 64 miles of extremely high tensile strength cable falling at terminal velocity…
Not quite sure where you got the 64 mile figure.
Also, while it’s falling straight down, it’s not going to burn on reentry, because it’s just falling down at terminal velocity. Sort of. That’s the end that’s tethered to the planet. Problem is that the top part IS at orbital velocity, which is why in a break failure, most of the cable wraps itself around the planet, and much of that will be traveling fast enough to burn up.
It depends on where the break is. The portion below the break will fall to earth, the remainder will rise to a slightly higher altitude, probably with a non-circular orbit. Both sections will be hazards, The upper section will be a hazard for a long time, a danger to space travelers until it’s repaired or towed away.
Physically, the tension release of the break in the cable will travel upward in the cable at the speed of sound in the cable (probably about 12,000 mph) so the movement of the center of gravity of the detached portion of the cable will likely accelerate over about 3 hours.
Cone-shaped until you get to the geosynchronous orbit, then tapering back down as you go out from there to the counterweight. This is a little counterintuitive, but in the limiting case, where you just use more cable as the counterweight (the same length as earth-to-geosynchronous orbit), then the force is zero at the far end, so it can taper back down. Not that anybody would build it that way, but the longer the counterweight end of the cable is, the smaller the counterweight can be, and the less tensile force there is at the end.
>” No rocket engines”
There has to be sideways thrust on the climber or otherwise coriolis forces will pull the whole cable down by stretching it sideways. Doing a pure vertical climb takes weeks or months becuse you have to move very slowly. Any sideways deflection of the cable is multiplied at the ends, so if you don’t account for the need to accelerate the climber horizontally, you’ll simpy yank the counterweight out of orbit or snap the cable.
The same effect happens when two satellites are tethered together and they start to pull in. Even if they don’t seem to be moving relative to one another at the beginning, if the satellites are moving just 1 m/min laterally when they’re 100 meters apart – an imperceptible crawl – conservation of momentum will make them spin like a carousel when they’re 1 meters apart.
Wonder if Kerbal can model space elevators?
I believe that is one of the “forbidden mods”, along with shooting elephants out of the rocket(s) for thrust.
My reading is it’s a limitation of the engine. They only model out so far (perfect for rockets and space stations). But a space elevator is a very big thing to model.
Computer models can model anything with whatever result you want to get if you ignore enough factors or just write the code wrong. Consider meteorological models, not good enough for reality (considering the accuracy engineers demand for their models) but good enough for broadcast and chicken little.
Meteorological models are good enough to model reality, it’s the data gathering ability of reality that has been the limiting factor. I understand that’s being worked on with some new satellites.
Often the models overlook some very basic things because they’re not trying to model the long term environment – just predict where the clouds will be 24 hours from now.
It’s one thing to model from physics first principles, and another thing to predict whether it’s going to rain or shine tomorrow.
If you’re talking about weather forecasting, the limitation is chaos theory. It’s well documented so I won’t go into it here. It will never be possible to predict beyond a fairly short period, even if you measured the position and momentum of every atom of air.
If you measured every atom, your prediction would be off because you would be also imparting an unknown momentum on every atom and fudge the results. You’d have to measure yourself to know how you disturbed the system, which would disturb yourself…
Coriolis force is definitely a problem, but I’ve never heard of anyone suggesting the climbers have horizontal rocket engines, or that the force would be so great it’s insurmountable.
Common thought seems to either climb slow enough that the forces don’t get strong enough to do any damage, or create a “two lane” tether. With one payload descending while another is ascending, the forces will counteract each other.
Consider you have a straight guitar string made of completely rigid nylon. A fly lands on the middle of the string – how much force on the string do you need to pull it straight again?
>”the forces will counteract each other.”
Yeah, if the payloads were of equal size and traveling like prayer beads all along the length of the cable. If there’s just two cabs one going up, one going down, they will make the cable go S-shaped.
Is the coriolis force present at the equator (where an elevator would be build)?
Yes. The coriolis force appears anywhere on earth.
The coriolis force appears whenever your velocity vector has a component perpedicular to the earth’s axis. That means there’s always one direction you can go – parallel to the axis – where your trajectory doesn’t seem to curve along the ground.
Yes you have to overcome lateral forces or you will pull the station out of orbit. You might as well use an airplane to get up where the air is thin first.
Not it is not Coriolis forces at the climber, it’s aerodynamic drag forces causing the deflection at the climber. Just a technical clarification. Coriolis at a global level causes wind effects which lead to the local aerodynamic drag forces. So you are half right, just depends on where you draw your set boundaries.
But the tether is fixed at a given place in the atmosphere, the climber does not move horizontally in relation to the air at any altitude (wind aside of course). At any given altitude, the climber will be moving horizontally exactly as fast as the ground. Geostationary orbit is simply an orbit that is high enough that a satellite can stay “up” while *only* moving as fast as the ground beneath it, in angular terms.
>”At any given altitude, the climber will be moving horizontally exactly as fast as the ground.”
Exactly, and that is the problem because they should be moving faster the higher up they go to remain horizontally over the same point of ground. The point on the ground is tracing a smaller circle than the point up at geosynchronous orbit in the same time it takes for the earth to rotate.
The angular velocity remains the same, but the speed of the climber doesn’t.
Yes it’s coriolis forces at the climber.
The climber has the angular velocity of the earth when they start at the root of the cable. As they ascend, the circle around the earth they’re traveling on gets larger and larger, but the climber is still travelling about 1000 mph horizontally like it did when it was on the ground, so it’s lagging behind the cable and thus the cable gets pulled sideways. The climber has to accelerate in the direction of earth’s rotation to climb straight up, and vice versa, anyone coming down the cable must fire retro-rockets in the opposite direction or else they’d twang the cable the other way.
Ignoring aerodynamics and the weight of the cable itself, to a first approximation the cable will have 2 perfectly straight sections, one section above the payload and one below. Sideways acceleration of the payload will be determined by the vector sum of the tension in the cable sections created by the angle between the two sections. No need for a sideways rocket as long as the cable has enough surplus length and sufficient tension. In any case the cable is going to be much heavier than the payload, which means the deflection is going to be fairly minor – though I’m not enough of a mechanical engineer to calculate the actual numbers in a reasonable amount of time.
“There has to be sideways thrust on the climber”
Or equivalent force on the cable at the ground, which is the idea. The cable leans slightly when a climber goes up, but an anchor at the ground provides the restoring force.
Obviously the climber gains a ton of momentum climbing the cable, which comes from the force on the Earth – so you’re (imperceptibly) slowing the Earth’s rotation.
It would take infinite force to keep the cable taut. Not having infinite force available, the cable must whip back and forth like a guitar string as loads are raised and lowered, and that creates some annoying oscillations at the counterweight which must also bob up and down in its orbit.
It takes infinite force to keep *anything* taut when it’s experiencing a load. Obviously the cable will bend somewhat, but its lean is *tiny* – less than a degree. Remember, the cable (plus any counterweight) is *massive* – you think of it as “light”, but it’s not, really. In any practical elevator it’s going to be on the order of ~1E6 kg. The climber just doesn’t exert enough force to deflect it significantly. “Whip back and forth” is an exaggeration when you’re talking about timescales of hours and deflections of fractions of a degree.
One of the easiest ways you can damp it is by using a second climber, launched at the right time and the right speed, to induce an opposite libration. Because the oscillation period is *slow* (hours) it’s relatively easy to predict and counter. You can even counter it with a single climber if you time its ascent properly, so that it’s essentially self-damping.
There are multiple academic papers studying this: just google “space elevator climber dynamics.” There are analytic solutions out there, too. It’s a tractable problem.
Yes. I’ve seen some of those calculations, and the result is that the climber has to run so slowly it takes a month to climb the cable.
Just as all geosynchronous communications satellites have to travel in equatorial orbits, Coriolis forces are avoided by building space elevators on the equator. For example, a suitable locations could be 14 miles north of Quito, Ecuador (shifted to the east or west as necessary). Many other suitable locations could be found in Africa and Indonesia. Quito is especially advantageous in that it has an altitude of 9350 feet, or almost two miles. Although this is a tiny fraction of the height of the space elevator, starting at such an altitude eliminates some of the worst problems with the atmosphere, as the atmospheric pressure is 28% less than at sea level.
Ecuador’s Chimborazo would be the one to pick: the point on earth furthest from the center. (https://en.wikipedia.org/wiki/Chimborazo ) At 6.2 km (whatever that is in ‘feet’) it’s even higher than Kilimanjaro, which might be second pick for elevator location (and Arthur Clarke’s choice).
Space Elevators will not work
1) The station is not anchored in space. Any force on it will move it.
1.A) weight + climbing force from the climber is a force that is pulling the station out of orbit.
1.B) Incidental or seemingly negligible deflection of the wire by wind will pull the station out of orbit. Given the angles and trig, the
2) #1 can be overcome by having continuously fired rockets to counteract the effects
2.A) This will be about equal the energy expended to just launch it the normal way
2.B) Because of Trig, this will be many many times greater energy expended than the energy causing the deflection.
3) Tension and snap dangers, (I see a movie plot forming here)
The more you strengthen the wire the more 1.B becomes a larger problem.
But really all of this can be distilled to it won’t work “Because physics”
Balance your forces, understand that PE = mgh, etc. If not I have a magical Bridge to sell you.
However there is the alternate and real objective, to sucker the investors who are bad at math/physics and live high on the hog until 2050 and beyond. It’s not about science, it’s about using science as a trick to score that sweet sweet VC.
” If not I have a magical Bridge to sell you.”
A bridge to LEO? Take my money, please!
Well, amusingly enough, a space elevator is actually not that big of a winner in terms of getting stuff to LEO. Once you get your satellite there, you need to accelerate it by 5km/sec in order to get it to stay there! Less fuel involved if you release in space of course, but still quite a bit.
Unless you have a particularly radiation-sensitive payload that can’t go more than a few hundred km up even while dormant, it’s more efficient to reach LEO by lifting it much farther, so when released it falls in an elliptical orbit with atmosphere-skimming perigee; a few aerobraking passes bring the apogee down to the desired orbit, then a short circularizing burn at the apogee lifts the perigee out of the atmosphere.
If the ground pulley applies a force, this can be reduced when a load is attached to the line so that the force to the (for the sake of argument, practically it will be in a different place) geosynchronous sat remains the same.
There are conservation of momentum issues and there is nothing wrong with sending a stream of space rocks back down to balance what is going up.
The mechanics works, but we still need a substance strong enough to make it from.
I don’t understand there wouldn’t be any substance strong enough for that. Let’s say I need to lift 10 pounds with a rope that can only handle 1 pound, I can put lots of them in parallel or built a bigger rope. I just don’t understand that issue. We can build bridges thanks to structures. Why not a big fat rope ?
The problem is the rope needing to support its own weight. Say you have a rope that breaks at 10 pounds, and weighs 1 pound per foot. Any hanging piece of it longer than 10 feet will break under its own weight, no matter how many of them you put in parallel.
You can extend it further than 10 feet by hanging a short single rope under a pair of ropes, which hang under 4 short ropes, which hang under 8, and so on. But the total material you need now grows exponentially with the length you need to reach. Try to make a space elevator out of existing materials, and you need billions of tons of stuff with a base that’s miles across.The problem is the rope needing to support its own weight. Say you have a rope that breaks at 10 pounds, and weighs 1 pound per foot. Any hanging piece of it longer than 10 feet will break under its own weight, no matter how many of them you put in parallel.
You can extend it further than 10 feet by hanging a short single rope under a pair of ropes, which hang under 4 short ropes, which hang under 8, and so on. But the total material you need now grows exponentially with the length you need to reach. Try to make a space elevator out of existing materials, and you need billions of tons of stuff in a column that’s miles across at its wide point.
And I apparently ^C^Ved out of reflex or something. Thanks for the nice edit button, Hackaday! It’s so easy to fix stupid errors now that you’ve added that.
>Any hanging piece of it longer than 10 feet will break under its own weight
In atmosphere use a helium or hydrogen balloon at 5 feet intervals to support a little over its weight. Out of atmosphere would be an issue, maybe gravity would be less.
The station is anchored in place by a tether & weight extending *past* geostationary orbit. Since the whole system is moving at the speed of geostationary orbit, the counter-balance weight exerts centrifugal force on the station (a higher orbit has a lower orbital velocity). You will require some delta-V to make corrections, but at geostationary orbit, these values are pretty low in terms of % of overall velocity. A LEO satellite has an orbital speed of almost 8 km/s, vs geosync’s speed of 3km/s.
The energy to lift the climber will be equivalent to that needed to push the same mass to orbit, yes. However, you don’t have to take rocket fuel with you, and accelerate THAT as well. Not to mention the fuel to take the fuel….etc. The rocket equation sucks, space elevators fix it.
Tether snapping is of course the major concern, but that was mentioned in the article. Materials science has a long way to come yet, so this engineering test is just that, a test.
2.A is bullshit.
First, a significant part of the energy in a conventional launch is spent countering the weight of the rocket, especially early in the flight where it’s fully fueled — only the excess thrust actually contributes progress to orbit. This effect, AKA “gravity drag”, accounts for perhaps 10% of delta-v, and thus thanks to the rocket equation, perhaps 20-30% of the fuel. For the space elevator case, though, the weight of the payload is borne by cable tension, not thrust. This benefit compounds — not only do we save the delta-v otherwise wasted on fighting gravity, but it allows us to use high-impulse, low-thrust engines, such as the various types of ion thruster, needing less propellant for the same delta-v.
Second, the propellant doesn’t have to be lifted to orbit from Earth. If it is, something very much like the rocket equation applies, since you’re still bringing your propellant to orbit with you — after all, it makes no difference whether each vehicle climbing the space elevator is 90% fuel and 10% payload, or you send 9 climbers full of fuel for each one full of payload. (The climbers themselves don’t count, since sending them back down empty cancels the effect of the climber’s own mass.) But if you bring your propellant from the lunar surface or asteroids, which are much closer (in delta-v) to GEO than Earth’s surface is, the elevator only needs to carry payloads.
Finally, once you can bring crap from the moon or asteroids to the elevator terminus, you don’t even need a way to use that crap as rocket propellant — just send it down the elevator to earth with your empty climbers, and the acceleration from deorbiting it cancels the deceleration from lifting a similar mass to orbit.
Of course, a terrestrial elevator remains a pipe dream (or a tool to fleece investors, as you say), if for no other reason than because materials science is nowhere close to making it work. Only a lunar elevator (which conveniently avoids atmospheric issues) is practical today, and without a lunar base to benefit from its capacity, there’s really no good reason to build one yet.
” the weight of the payload is borne by cable tension”
LOL, nope. At best you move the thrusters to the station so it doesn’t get pulled out of orbit.
I agree. This is a crackpot scheme that has been kicking around for a while now, but basic physics will keep it from ever being a reality. Tesla’s ring around the world that floats by the forces of gravity is a better idea, but equally not possible due to materials limitations.. At least his idea could be used for both power generation and global travel and shipping.
It’s curious that no one talks about orbital rings that much. A true orbital ring, though a huge project, seems to me not only more feasible, but more useful than a space elevator or two. (As you say, a network of orbital rings a couple hundred miles up could essentially replace air travel and carry solar power down efficiently. Also, host wireless transceivers, carry intercontinental fiber optic lines…)
What do you mean materials limitations though? IIRC, something like a thin aluminum cable could work for a minimal initial ring. And you’d “only” need to launch something like 20-200 kilotons worth of material for that sort of bootstrap system.
“What do you mean materials limitations though?”
AIUI, there is no material on Earth that can support 100 miles of its own length.
Definitely way more feasible than a geosynchronous elevator, but definitely has hundreds of extremely non-trivial engineering challenges that are almost always ignored. We have lots of issues designing large bridges over water, and spend billions on relatively mundane terrestrial infrastructure projects. Imagine an unwanted resonance building up in something this big. How’d you manage that? And if it falls it’s going to cause a minor impact winter and glass several equatorial countries.
Guaranteed it would still be at least a couple orders of magnitude more difficult and expensive to build than any expert today expects. We’d find huge problems as we go.
This all sounds the same as “aeroplanes won’t work because physics” yeah, if we apply half the physics we know to demonstrating the problems and forget the other half we already know that can be applied to solve them.
Total myth. People knew of the existence of birds back then, so clearly nobody competent was saying powered heavier-than-air flight was against the laws of physics. It’s a bad analogy, just like the myth that breaking the sound barrier was considered as impossible as we now consider the light barrier. No credible scientist ever claimed that back then, and those things are fundamentally different.
That’s kinda the point, nobody credible is calling this impossible now.
Plenty of credible people are correct to point out the lack of any form of solid matter with the required tensile strength.
Right. Nobody’s calling it impossible. Just a bad, bad idea.
Crossing the sound barrier was considered impossible because it WAS impossible.
People knew perfectly well that rockets and bullets etc. went beyond the speed of sound, but they also knew that an airplane couldn’t because a prop stops producing thrust after the blade speed goes beyond the speed of sound, because it cannot propagate a pressure wave behind itself – it just becomes an air brake. An airplane could temporarily break the sound barrier in a dive, but that was it.
Rockets were obviously considered impractical (although the Nazis did try them), so it wasn’t until the invention of the jet turbine that supersonic flight became actually physically plausible.
I’m not sure I understand… because axial flow gas turbines were required to bring the rocket up to a higher speed before launch? The first planes that broke the sound barrier were rockets…, albeit dropped from aircraft for the most part. Instead of a rocket assisted takeoff are you meaning more of a jet plane assisted takeoff?
Propellers do lose efficiency with increasing mach number, but the mach number at the tips is always higher (due to the propeller’s rotational speed) than that for the aircraft; there’s no effect where the propeller suddenly stops giving thrust, but even if there were, it would not correspond to the “sound barrier”. In fact propellers can easily see transonic flow while the aircraft is very subsonic. Thin, cambered blades are the best choices when one need a prop to deliver good performance with transonic flow, though it’s usually better to use a smaller diameter prop (lowering tip speed) with more blades and avoid the transonic regime.
Note that the XF-84H, surely the best known example of a propeller designed for and operated in the supersonic regime, did in fact fly. The plane was not successful for a number of reasons, but the fact that it flew at all is absolute proof that a supersonic prop is not “just an air brake”.
When the entire prop meets an airflow faster than sound, its efficiency essentially drops to zero. It cannot produce thrust because pressure waves in a supersonic stream can’t travel “upstream” – it’s moving away from the propeller faster than the air molecules can vibrate in the opposite direction, so they never touch the backside of the propeller blade and there’s no reaction force forwards.
Jets work because they have a constriction nozzle that turns the exhaust stream supersonic.
Nonsense. Propellers are made of airfoils. Clearly there have been airfoils created that produce lift at supersonic speeds, so if you want a prop that generates thrust in the supersonic regime, you just need to design it for that.
The XF-84H is a turboprop craft, which derives part of its thrust from the jet. It didn’t go over the speed of sound at level flight (its desing speed was Mach 0.9, tested at Mach 0.7), and it couldn’t derive any thrust from the prop when it was pushed supersonic by diving.
As long as the counterbalance is heavy enough and far enough out, perturbations are self-correcting. The difficulties in space elevators are materials science and assembly.
So far, long tether lines have had bad habits in space. However, shorter lines had been used to stabilize a few satellites. If you link 2 objects in orbit but at different altitudes, the theory runs (or ran) that running a current across the line and across the Earth’s magnetic field would allow a more active altitude control.
I think the Japanese had such an experiment a few years ago.
You may be thinking of the Italian satellite, more than 20 years ago. And 22 km long tether. http://www.astronautix.com/t/tss.html
It was not the first one either, there’s been a number of space tether experiments:
https://en.wikipedia.org/wiki/Space_tether_missions
This is a great read if anyone is interested: http://a.co/d/d79CTRL (“Space Elevator Survivability Space Debris Mitigation”)
200 hundred kilometers per hour, that’s pretty fast.
Compared to, say, rowing across the atlantic, yes, 200 km to geostationary is fast. But it’s still a one-week trip. Dunno about you, but the 18-hour trip from Dallas to Sydney in an airbus is trying enough. I can’t imagine being stuffed in a passenger capsule for a week.
200 km per hour, of course. oh, for an edit button…
So what if it’s a long flight? Non-human payloads won’t care. And how much prep time is expended before the few minutes of flight in a rocket launch? I suspect the elevator will still a significant net win in time on top of money.
As for humans…think about what accommodations are like on the ISS. Anything on the spectrum of ‘submarine’ to ‘dorm room’ should be more than adequate. Heck, make a real ‘cruise ship’ for the tourists. Maybe with a stop partway up for the ones with parachutes. :D
In order to get to geo stationary, you have to pass thru the Van Allen radiation. Hopefully you’re not ‘riding leisurely’ in there for too long…
One (of many) thoughts about the craft riding the elevator is that it won’t carry its own fuel, so it’ll be able to have significant shielding.
Yeah, and if it’s an issue for the climbers, it’s an even bigger issue for the cable, portions of which would have to not just pass through periodically, but actually bathe in that radiation continuously for their entire service life.
AFAIK, very few, if any, materials would be able to retain any useful properties in that kind of bombardment environment for long. And you don’t just need any material, but an exotic, ultra high-strength one capable of suspending it’s own weight from 36 million meters. IIRC, boron-nitride nanotubes are somewhat more radiation resistan than the carbon versions that are usually bandied about as a hypothetical material, but even those may not be good enough. If you have to replacing cables too often, it’s going to hurt the economics of the thing.
Some kind of lightweight (replaceable?) polymer shielding might help, but that obviously drops the strength-to-weight ratio. I suppose some kind of electrostatic or magnetic shielding might be a solution. The field would have to be safe for climbers to pass through. And you’d have to figure out how to interact with the magnetosphere in just the right way.
Lots of engineering still to be done there. A theoretically strong enough cable might be the least of it.
Lol thats just mostly bullshit.
Firstly, this experiment is “trivial“ engineering (albeit I must acknowledge the art of doing it). We do not learn anything from it about building space elevators. Actually IMHO this weird experiment does not zeach us anything.
As you pointed out the challenge is in big parts the material science of building the cable and thats what money should be invested in.
And just some general thing: Only if there is some company which claims to be able to realize some utopic goal in 50 years does not suggest its possible. Hell, there have been companies claiming perpetuum mobiles or reactionless drives. Those guys are probably just idiots.
Also your comparison to faster than light travel is highly inappropriate. You liken weird science fiction theories (of which you claim to understand the “principles“) to some highly involved engineering problem. Building a space elevator can be seriously discussed, but sorry, faster than light travel is just unphysical nonsense.
Ive read better articles here.
Alcubierre lays out a decent pathway, admittedly being able to create (perhaps more importantly end) the warp bubble is far from understood but we have a decent idea of the energies involved. Roughly the energy held in a mass on the order of Jupiter the last time I checked.
Ending one of those warp bubbles is predicted to send a stream of extremely high energy particles in the direction of travel as well, so you need to be extremely careful not to actually point your vessel at where you want to go for fear of sterilising it with radiation.
If you think that space elevators face anything resembling the sort of problems as cold fusion and faster-than-light travel, then no, you don’t understand a damn thing about the principles required for them. Space elevators merely require nano-unobtanium materials, the absence of orbital debris, and utterly impractical mega-construction projects. Cold fusion and superluminal travel require substituting fantasy for physics.
Or an understanding of physics we currently don’t have.
Nah. There are some things that new physics are almost certainly never going to help us with.
The Alcubierre drive is theoretical, but the math has held up to scrutiny so far.
Enough that NASA recognizes it enough to work on a warp-field interferometer. It’s just something we can’t build yet, probably not for centuries because of the energy requirements.
Its not fantasy, it’s technology beyond our civilization’s current tech. The same as space elevators, but even farther out.
You forgot the part of the Alcubierre drive that requires negative mass. Getting it down to the point of only requiring a planet’s mass worth of energy requires first having invented antigravity. It’s worth noting that most of NASA is embarrassed about Harold White’s bullshit, but he only turned crackpot after getting hired to a nigh-unfireable public service job, so NASA prefers to humor him rather than publicly admit that they want to fire him but can’t.
Negative mass != anti-gravity.
Mass is independent of gravity so the two are quite different. The effects may be indistinguishable on the macro-scale (assuming negative mass doesn’t also reverse the arrow of time as some postulate) but they are not the same.
The existence/possibility of negative mass is hypothetical physics. It hasn’t even been shown to exist in a theoretical sense.
It’s not negative mass, it’s negative energy density. The difference comes about because of the possibility of altering the ground state – so you’re not creating ‘negative mass’ such as suppressing modes creating a ground state with less energy than the normal quantum vacuum. More specifically, it’s violation of the weak energy condition, which *has* been shown to exist due to quantum effects, such as the region between plates in the Casimir effect.
The *idea* isn’t hypothetical physics, it’s just there’s no known way to generate *large-scale* violations of the weak-energy condition. But it’s not hypothetical in the “fairies and unicorns” sense.
So we’d just need some plates very close together? That’s much nicer than exploding Jupiter every time you want to go somewhere.
The math kinda works if you assume the existence of negative energy density. One thing the math doesn’t work out: Once the “warp bubble” is in place, the curvature makes it so that no matter or information can reach it from the inside without exceeding the speed of light in a vacuum through flat space-time. So how do you steer, or even stop for that matter?
There’s also a hypothesis that it sweeps up and traps photons and particles in its path and traps them, which over the light-years adds up and probably cooks the occupants and belches out a planet-killing gamma ray burst at the destination.
And it still allows communication between two parts of the universe faster than a photon would travel through a flat vacuum, which breaks causality no matter how it happens. You can have causality, relativity, or FTL. Pick two. We are already extremely certain about relativity, and breaking causality is logically absurd and has never ever been observed, even when astronomical amounts of energy and violently twisted space-time is involved. I wouldn’t bet on it.
Kind of “fuzzy” on causality.
https://physicsworld.com/a/quantum-mechanics-defies-causal-order-experiment-confirms/
Quantum scale maybe, people scale–that would be truly incredible. It would represent about the only hope left for FTL.
BTW, the 36Mm distance is valid only if you want to put the station at geosynchronous orbit. That’s the main problem. If the end of the cable was closer, you’d avoid the issue with the strength of the cable + debris. You can have a closer end to the planet, if you had, say, a sufficiently massive object at geosynchronous orbit and place the cable’s end on the first Lagrange point between Earth and this utterly massive object. For this object to provide pseudo L1 stability, it should be at less than 1/25 the mass of Earth (easy) but the complete lift system would have to also be multiple order of magnitude less heavy than the end station. The heavier this object, the farther the L1 point to the object, and the closer to Earth the end station.
Then the elevator would not be sustained by centripetal force, but by gravity, providing less stress on the material, so maybe it’s possible to build such material.
The main issue with this scheme is how to “upload” so much mass up there first (as also, how to accelerate it to orbital speed), which is a catch 22 scheme by itself. Maybe in the future we can “download” some asteroid down to geosynchronous orbit so avoid paying for the gravity well’s energy required to lift that up.
To give number here to have a feeling of the difficulty, the moon that’s 1/80th the weight of Earth and located at 385Mm from Earth provide a L1 point at 321Mm from Earth.
If it were at 36Mm from Earth (on geostationnary orbit), the L1 point would be at 30Mm, that’s where the end station should be.
Not sure anyone would want a moon so close anyway, just to gain 6000km (20%) of cable.
Another idea is also found in SF, is to have a cable not connected to ground (hanging in the sky) but attached to a much closer satellite.
You’d use a regular plane with aerodynamic forces to lift the payload and hook it up on the cable. The station would then rotate and let the other end of the cable fall down to earth while the hooked end is being lifted. This is called Skyhook and is probably more realizable.
Very interesting concept. The experience from what JAXA learns will hopefully help us and the rest of the world as we overcome the complexities of space travel.
Let’s not forget Robert L. Foward’s contributions to the field too. Inventor of (among other things) the Forward Mass Detector (gravity gradient sensor), and founder of Tethers Unlimited http://www.tethers.com/ Decent hard sci-fi author too.
By the way, the assumption seems to be that the “top floor” is in geosynchronous orbit, this isn’t really true. The center of mass of the entire system needs to be in geosynchronous orbit, which may require counterweighting some distance up from the “top floor”.
Space elevator to geo synchronous orbit is sub 90 IQ, and completely impossible unless we can make some molecular assembly machine that can print and align 100 mile long graphene nano ribbons or carbyne while placing some sort of elastomeric buffer between them so they don’t cut each other, highly unlikely. Space elevator to orbital ring in LEO is doable fairly cheaply with UHMWPE cables and makes way more sense, costs around 10 billion dollars. Then you just use mag trains to accelerate rockets to orbital speed. If you don’t get it, don’t comment below look it up very simple concept to understand that is an orbital ring and that this concept of geo-stationary elevators is brain-let tier thinking in our gravity well.
Your references to iq and the term “brainlet” are all anyone needs to see you’re full of it and likely don’t have as much of a grasp on what you’re saying as you think you do.
Do you really think an actively-stabilized ring around the entire planet would have no unsolved engineering issues and would cost only ten billion? That’s so absurd.
Elevator to orbital ring might be feasible and indeed cost mere 10 billion dollars. Now, if we only had an orbital ring…
I’d want it to work, but a ring with circumference of some 41000 – 46000 km that would not get crushed under its own weight is well in sci-fi territory. Spinning the ring up at orbital velocity would make it all more plausible, but still nowhere near realistic.
Besides, who in their right mind would build a megastructure that’s labile, nearly touching earth’s surface and spinning at some 8 km/second? A small problem with the active stabilization system would cause global destruction. (On my rough estimate: it might be comparable to an all-out nuclear war, or possibly more destructive. To get a better estimate, one could estimate the mass of the ring, calculate it’s rotational energy and then refer to the handy Boom Table at http://www.projectrho.com/public_html/rocket/usefultables.php )
This sounds like a great idea to make it easy to land on/get off the moon or mars. Then once that works you’re way closer to figuring out how to do the same thing on earth.
Mars, yes: about the same rotation period as earth, but one third the gravity.
Moon: nope. Despite the 1/6th gravity, the rotation period is four weeks, making the tether unreasonably long (and I’m guessing also perturbed into destruction by nearby Earth.)
In case it’s not obvious, guess how far from the moon its selenostationary orbit is. Hint: it’s the distance at which you always see just one side of it.
A lunar space elevator from one of the poles to L1 (50,000km out) has been proposed as a near-ish term goal. Supposedly it can be done with current material sciences, should anyone be so inclined to spend the money.
https://en.wikipedia.org/wiki/Lunar_space_elevator
Sure, if you just naively calculate a “selenostationary orbit”, it’s outside the Moon’s Hill sphere and gets yoinked by Earth. But could we use Earth’s pull to our advantage? If only there were well-known studies of the three-body problem, with points of stability for a third body of negligible mass known for a couple centuries….
In case it’s not obvious, you run the cable through, and place the counterweight just beyond, the L1 or L2 point of the Earth-Moon system.
Correct me if I’m wrong, but doesn’t the Earth/Moon Lagrange point stay aligned with the centres of both bodies? i.e. not aligned with a single point on Earth, as required for a ground station?
Ben was referring to a lunar space elevator. Not a terrestrial one.
I’m glad Tom and ben demonstrate that there are some rational posts in this thread.
(and, yeah, I blew it, forgetting about the Lagrange points)
isnt a space elevator supposed to be made out of diamond extracted from one of the moons of Jupiter
They’re deliberately avoiding that scenario. Azimov’s estate attorneys would welcome such a proposal.
Arthur C. Clarke also proposed something like this at the end of 2061: Odyssey Three (I think). He described a native of Europa orbiting the new Jupiter star looking up at the sky and seeing the diamond lattices created by humans.
D’oh!
I meant Clarke!
Thanks!
“Space elevators belong to that class of technology that we all want to see become a reality within our lifetimes, but deep-down doubt we’ll ever get to witness firsthand. Like cold fusion, or faster than light travel, we understand the principles that should make these concepts possible, but they’re so far beyond our technical understanding that they might as well be fantasy.”
You group the technological feasibility of a space elevator with faster than light travel? When it comes to FTL travel, we’re not sure if physics even would hold for this, because we’re getting into some weird shit. When it comes to space elevators, the main problem we don’t know how to solve yet is a material for the tether. Other than that, we have all of the technology identified. Such a material might not be possible, but it definitely seems less far-fetched than FTL travel.
As for “cold fusion”, wasn’t there an Italian guy who solved that? :P Whatever happened to him, btw?
The Mafia “put him on ice”.
actually, the funniest part of this article was the “$90 billion USD” – if that is all it cost it would be built tomorrow… Maybe you meant to say “90 trillion USD”….
I saw this post and it reminded me of the What-If XKCD comic:
https://what-if.xkcd.com/157/
It’s magical! How the station will keep it’s speed if it’s take a load at lower speed from earth? Look like impossible without lifting a lot of energy from earth.
Anyway amazing project
Quote: Space elevators belong to that class of technology that we all want to see become a reality within our lifetimes….
Do you belong to some strange cult, one you never leave? That remark is sheer idiocy. Most people, a big slice of any “we all” remark, have never thought about the topic. And most, it’s easy to believe, would consider it utter idiocy. What’s going to happen, for instance, when that long cable grows old and must be brought down?
Space elevator nuts—for that’s what they are—gush about how much cheaper it would make getting into space. It apparently never occurs to them that given how cluttered the space around the earth is becoming, that we need to make getting there difficult and that one way to do that is to keep it relatively expensive. The cost itself will discourage orbiting devices that are of little value.
harsh, but fair.
One of the rarely-mentioned risks having to do with these astronomical megastructures is that even if we did manage to succeed and make one, it would carry a correspondingly astronomical amount of potential energy. If it ever fell–and it absolutely would eventually fall, such a precarious thing operating on the razor’s edge of physics and materials science–it would represent a release of energy on par with a major impact or a global thermonuclear war. Simulations show a space elevator would whip about and wrap around the equator if it fell. It would be far too much of a risk to allow such astroengineering projects to be built close to Earth. Not that we have the materials or budget anyway. The estimates for budget are always massively optimistic, too. Probably orders of magnitude off, even before you consider the civilization-ending disaster that happens when it all goes sideways.
http://gassend.net/spaceelevator/breaks/
It sounds all fine and dandy until an aircraft runs into the cable.
…Or the whole thing goes all Tacoma Narrows Bridge on us.
That’s the big issue I see with the ring idea, getting tidal and orbital perturbations under control in that so it doesn’t flop flop smash.
… and there needs to be an excuse to start a war somewhere to extract more raw materials even though we have plenty of thermite embedded in the insulation?
“…Like cold fusion, or faster than light travel, we understand the principles that should make these concepts possible…”.
“We do?” “WE DO“?
This is the kind of pathetic horseshit that completely shuts down our attempts to teach–and give a zeal for–real science to young children, and why so many adults are dumber than a box of rocks when it comes to anything having to do with science…other than, possibly, ‘ear-candling’.
Exactly WHAT PRINCIPLES should make cold fusion and faster-than-light travel possible? The same principles that SHOULD make a perpetual-motion machine possible?…that allows, beyond a shadow of a doubt, for the reversal of entropy?…that proves that time-travel is possible?…that absolutely proves that N-Rays DO exist (you ARE familiar with “N-Rays”, aren’t you?).
I strongly suggest that you familiarize yourself with the the following books:
Why People Believe Weird Things: Pseudoscience, Superstition, and Other Confusions of Our Time; ISBN 1-56731-359-0, by Michael Shermer, with foreword by Stephen Jay Gould.
Weird Water & Fuzzy Logic: More Notes of a Fringe Watcher, Martin Gardner;
ISBN 1573920967 (ISBN13: 9781573920964)
I suspect you’ve taken a little jovial journalisting entirely too seriously. I suspect the ‘cold’ in ‘cold fusion’ shouldn’t be there, but otherwise there are theoretical frameworks for all the concepts mentioned in the article.
There is absolutely no such thing as “jovial journalisting” unless it is specifically identified as such, either by the reputation of the author as a humorist, or by the type of the publication. Where, and when, were you informed that this article was ‘jovial”, that the author is known–and wrote this as–as a humorist, or that this publication is not supposed to be a serious one; that it is not for enlightenment, but for humor.? I have every confidence that when one of Hackaday’s authors or editors offers something up as humor, it will be identified as such (occasional slips, such as claiming that a certain South African blow-hard is the greatest person ever, can be written off as brain-farts, and not absolute stupidity…unless it happens more than once).
Please enlighten us as to the ‘theoretical framework[s]’ for faster-than-light travel. Sounds to me as though you have a sterling future in the field of physics.
Read the books.
“Whenever anyone says, ‘theoretically,’ they really mean, ‘not really’.”— David L. Parnas
Your inability to detect humour is your own failing, don’t lash out at me.
A theoretical framework for apparent faster than light travel is the Alcubierre drive. It’s a current theory which has so far not been falsified.
I never said that I have an inability to detect humor; you say that. What I did say is that …”I have every confidence that when one of Hackaday’s authors or editors offers something up as humor, it will be identified as such…”.
To demonstrate to you my exquisitely finely-honed sense of humor, my amusement at the Alcubierre drive example which, like string theory, only requires–for validation–more energy than exists in the known universe, provides me–as well as others, including physicists, I’m sure–with an immense amount of laughter.
“…It’s a current theory which has so far not been falsified.”.
Not even close to a polished recommendation. Not even a ‘side-ways’ compliment. Reminiscent of Wolfgang Pauli’s statement that, “…that’s so bad, it’s not even wrong…” (as I understand it, Pauli made this comment precisely about a conjecture which could not be falsified).
Any ‘theory’ which can NOT be falsified is not a ‘theory’, and is not even considered worthy of consideration by
most seriousphysicists. This, for your information, is one of the stumbling blocks regarding string theory: it cannot be falsified.But enough of our ‘shop talk’– thanks for this humorous interlude.
You’re right. That’s why only trained professional comedians ever tell jokes, at times and places especially denoted for the purpose.
Hitler? Is that you?
Why not just read the other comments? There’s definitely solid theories on FTL drive, but it’s at least a century beyond our current tech. Space elevators are also something we understand, but can’t currently build because of material limitations.
It’s a valid comparison, you are just being exceptionally obtuse for some reason.
“Why not just read the other comments? There’s definitely solid theories on FTL drive…”.
You’re absolutely correct, Just not any solid theories from anyone with a physics, scientific, or even degreed-engineering background.
FYI: personal opinions don’t count as “…solid theories…”; only as “…Hey, look at me; I made it into the ‘comments section’…
Relax, it’s just clickbait. :)
The space elevator will never be built, but it will create clickbait for ever.
I have been giving a lot of thought to this problem–
Exactly WHAT is Elon Musk’s next great diversionary tactic to deflect attention from the fact that he can not deliver, and IS not delivering on all the promises which he has already made (claims by certain people that Musk is one of the greatest individuals ever notwithstanding). Let’s face it: how many more “pedo guy” situations can be dropped into his lap? How many more bricks and flame-throwers can he peddle? (perhaps I’m a bit hasty regarding the “pedo-guy” thing; all one has to do is incur Musk’s wrath by telling him that he’s only in something as a ‘PR stunt’, and you’ll have your next “pedo-guy” situation).
The next Great American Musk Con is right here and, by jove, fits right in with all his other hare-brained, but imminently successful schemes at getting you to forget that he has yet to turn a profit. At anything. Except sucking up taxpayers’ money.
The next Musk-Con? The Musk Space Elevator , of course, It’s got Musk written all over it. Don’t believe it. Just have someone send Musk a copy of this Hackaday article.
And now imagine earthquakes like the one ruining Fukushima, that alters Earth’s rotational speed. Can you even imagine the tensile forces generated in a 72+ thousand kilometers long “bridge”, one end of which suddenly starts moving at, for example, 50 meters a day? How about oscillations coming from vibrations, generated by the moving cargo? Even if the climbers move inside evacuated maglev tubes there will be “recoil” forces as you accelerate / decelerate the carriages. And the carriages will have to be HUGE once you start hauling people by dozens, when you need them to endure a trip taking DAYS at a time. I’m speaking of air, catering, waste management, hygiene, etc. Pack a hundred people into a climber and it will have to be the size of a steamboat.
Musk can do it. Just ask him.
Nobody mentioned changing the gravitational constant, to reach space and eleminate all problems. Well, generating new problems.
Wasn’t there an attempt 10 or 15 years ago to trail out a long wire from a sat that used centrifugal force to keep it straight, and it was supposed to generate electricity by passing through the magnetic field as the sat orbited the earth? If I recall, it sort of succeeded and sort of failed — by generating a whole lot of electricity very briefly and burning apart.
This can happen if a thetered cable can be lowered to earth at a safe distance where an aircraft will attach to a capsule then hoisted to the hovering space station. Connecting earth to the hovering station might not be possible as the weight can pull back the entire station crashing to earth. When the capsule is attached much like air refueling system then it can be pulled towards the space station. This can be a start of building an entire scpace colony that can help save mankind when the ultimate catastrophe comes.
There’s a class of space elevators that operate similar to this. I read about them in a sci-fi novel many years ago. Might have been something by Larry Niven. By operating at a lower orbit, they have cables that aren’t as long and don’t need to be as strong. They aren’t geosynchronous, of course, but rotate continuously, at an appropriate speed so that an end dips down into the atmosphere periodically. I.e., the rotation of the cable is counter to the orbital motion so that the tip speed hits zero at the vertical position. There is some friction involved, but not that much because most of the motion in atmosphere is vertical, but this is compensated for with jet engines that operate while the end is in atmosphere. In the story, the cables dipped very nearly down to the surface, into stations designed to hitch the load to the cable. But it would probably be safer to have these only dip down to 10-20 km altitude and use air transfer, kind of like the mail hooks on ancient American trains that allowed mail to be transferred without stopping the train. Doing the transfer in the air also reduces the geopolitical issues involved with dependence on earth stations that have to be located on the equator – the transfers can be done over the oceans.