I find that if I’m trying to make a point with a student or a colleague about a circuit, sometimes the Falstad online simulator is worth a few thousand words. You can draw the circuit, play with the values, and even see the current flow in an intuitive way as well as make traditional measurements. The simulator not only handles analog but also digital circuits. At first glance, though, the digital functions appear limited, but if you dig deeper, there is a custom logic block that can really help. I dug into this — and into how switches work in the simulator — the other day in response to a Hackaday post. If you use Falstad, read on!

Childhood Memories

When I was a kid, I saw a computer advertised in the Layfayette catalog. It was the Geniac — the subject of a recent post about a recreation of the computer. My parents shelled out the $20 and I was excited. After all, the thing could play tic tac toe, compose music, and do other feats of wonder.

The problem is, no one that I asked — including an electrical engineer from the power company my Dad worked for — could figure it out. Keep in mind, I was probably 9 years old and back then very few people — even power engineers — were very computer savvy.

By the time I was a teenager, I realized the whole thing was a bunch of rotary switches you could configure as logic gates. By that time, though, the Geniac was long gone, a victim of Mom’s spring cleaning. A few years ago, I bought a mostly complete one on eBay but it needs lightbulbs that I haven’t replaced yet, but it is on my long list of things to do to get it working.

The Virtue of Shame

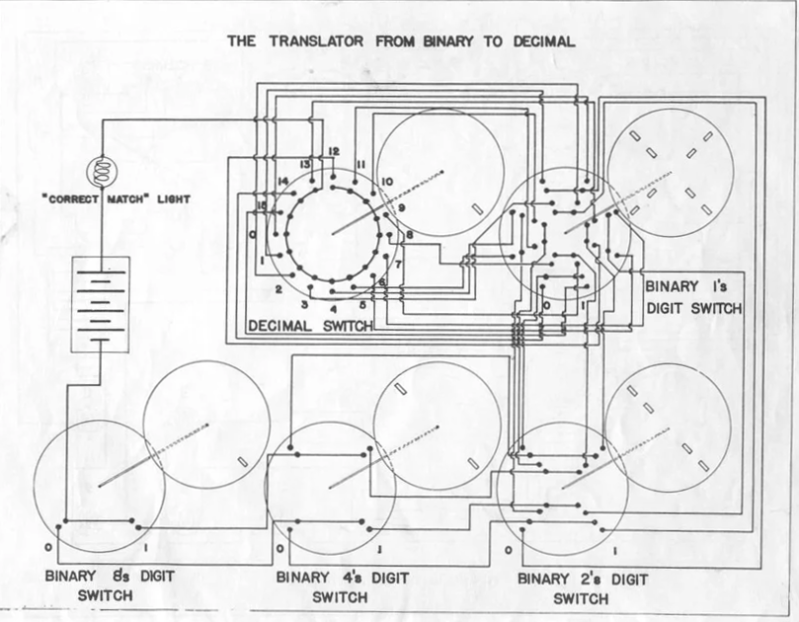
However, the Hackaday post shamed me into action. All these years and I haven’t built any of the circuits in the manual. I decided that I wanted to do that and since the post had a picture of the binary to decimal decoder, I thought maybe I could simulate it.

The key to understanding the diagrams in the Geniac manual is that you are building a multiway switch. So the binary 8s digit switch in the lower left of the diagram is a two-position switch. The binary 4s digit is DPDT switch. If you point at 0, the contacts at 7:00 and 1:00 connect. If you point at 1:00, the contacts at 5:00 and 11:00 short because of the brass staples in the upper disk. The decimal switch, on the other hand, is a single pole, but has 16 positions.

In operation, you dial in the binary number you want to convert and then turn the decimal switch until the light bulb turns on. This is a simple switch tree so that each binary number grounds one terminal of the decimal switch and since the lightbulb connects to the common, it lights up when you make that connection.

Falstad

There were two problems I had to tackle. First is making multipole switches in the simulator. There’s a way to do it, but also there’s a thing or two to keep in mind. The second issue was that I wanted to add a fancy display but a 16:1 decoder isn’t available. That’s how I got started with the custom logic block.

The switches are pretty easy to figure out. Under Passive Components on the menu there is an SPDT switch you can insert or you can use the uppercase S shortcut key. Of course, you don’t want a SPDT switch, but you have to start there. Once you place one on the screen, you can right click it and select Edit.

There are two fields in the resulting dialog box of interest. The number of throws is pretty obvious. For the decimal switch you can set that to 16. The switch group is the key to making multiple poles. Switch group 0 is special and means the switch is independent. However, if you set the group number to something else, all switches in that group will operate together. There’s no direct indication of that on the screen, though, like there would be in a real schematic.

Well, that’s not exactly true. Any switch that has more than one pole will show up as DP when you hover the mouse over it. So three switches in the same group with 16 throws will all show up as DP16T even though that’s not technically correct.

A Small Gotcha

The other thing I found by accident is that if you add a pole to a switch, you should make sure that the switch is in its default position and in the same orientation as the other switches in the same group. If you have the 16 position switch set to position 5, for example, and create a new switch set on position 0 then the switches will maintain that separation. That is, moving the first switch to position 6 will set the second switch to position 1. There might be times that’s a feature, but in general, it isn’t what you want. The real problem arises when you have the switches facing opposite each other. Then moving one switch up a position will move the other one down. Again, probably not what you want.

The switch has a way to set some sliders, but those sliders control the number of throws and the switch group for the switch so that’s not very useful. Probably the easiest thing to do is duplicate the existing switch to make a new pole.

Custom Logic

Armed with a way to make big switches like Geniac, it was pretty easy to set the switches up for the decimal converter. However, I wasn’t happy with it because the switches are hard to read. Falstad isn’t really made for 16 throw switches.

I wanted to take a second pole for the decimal switch and use that to drive a 7 segment display to indicate the position of the decimal switch. In order to do that, you need a 16 line to 4 line encoder but Falstad doesn’t have one that I could find.

You could build it out of logic gates, of course, but that would be tedious at best. But I noticed the block named custom logic (under Digital Chips) and that was the answer I was looking for.

When you place the block, you get a little box with a few inputs and an output. Right click and hit edit and you’ll see a box that lets you name a model to use for the function. Pressing Edit Model lets you change the function for blocks that use that model.

There are three defining fields in the dialog box. The first is the inputs separated by commas. You can use one or two character names. Another box contains comma-separated outputs using the same one or two characters. The box will redraw to fit the number of ports. There’s also an info text that shows up when you float your cursor over the box. The port names can also have a slash in front (like /Q) to indicate negative logic if you like.

However, the final field is the one you want. You can define your custom function using a simple syntax. Let’s take a simple example first. Suppose you wanted to build a block that was an AND gate with two inputs A and B. The output is C. The definition would be:

00=0
01=0
10=0
11=1

That’s it. In addition to 1 and 0 you can use + or – for a positive or negative transition. You can use pattern letters and you can use ? for a don’t care. For example, suppose you have a block that copies the first input (A) to the output if the Enable pin is true. If the Enable pin is false, you want to output a zero:

?1=A
?0=0

Or you could write:

00=0
01=1
11=1

The input string can be longer than the number of inputs. In that case, the simulator reads the outputs. This lets you build state. For example, the manual shows an SR latch with inputs S and R might have outputs Q and /Q:

??00=10
10??=10
01??=01
??AB=AB

The first line handles the reset condition so that /Q is always equal to the inverse of Q. It appears that in the definition you can name the outputs anything you want on the left and then use them on the right even if the port names are different (e.g., in this case, Q is A and /Q is B). That line could just as well read ??XY=XY. In the definition, you can’t use two characters including the slash.

The Final Product

Now it is easy to create the decoder:

0000000000000001=0000
0000000000000010=0001
0000000000000100=0010
0000000000001000=0011
0000000000010000=0100
0000000000100000=0101
0000000001000000=0110
0000000010000000=0111
0000000100000000=1000
0000001000000000=1001
0000010000000000=1010
0000100000000000=1011
0001000000000000=1100
0010000000000000=1101
0100000000000000=1110
1000000000000000=1111
????????????????=0000

The rest is just a lot of wiring. Although the snake of switch connections isn’t as aesthetic as the Geniac disks, it serves the same purpose. It would be a lot of work, but you could probably do all the other Geniac programs in the same way by noting how many throws and poles each disk switch has.

There are actually better ways than the Geniac to do computing with switches. And if you want to do more conventional logic simulation with Falstad, try building flip flops.