The current state of the art of embedded motion sensing is based around micro-electromechanical systems (MEMS) devices. These miracles of microfabrication use tiny silicon structures, configured to detect acceleration and rotational velocity in three dimensions. Accumulate these accelerations and rotations, and you’ve got a device that can find its orientation and track movement without any external waypoints. This is the basis of the technique of dead reckoning.

Why do we care about dead reckoning anyway? Surely GPS and related positioning systems are good enough? Above ground GPS is usually good enough, but underwater and underground this simply won’t work. Even heading indoors has a dramatic effect on the GPS signal strength, so yes, we need another way for some applications.

Right now, the current state of the art in portable sensors are MEMS devices, and you can get them for the cost of a hamburger. But if you want the ultimate in accuracy, you’ll want a quantum atomic interferometer. What that is, and how it will be possible to make one small enough to be useful, is half of the story. But first, let’s talk MEMS.

Fusion of The Sensors

Given an initial position and accumulated accelerations in 3D, it is possible to track position, for a short while at least. According to this (outdated) Cambridge University report on Inertial navigation systems, with a MEMS-based inertial tracking system, positional error can exceed 150 meters in under a minute, because the errors don’t average out, they accumulate.

Improvements can be made by fusing data from other sensors into the navigation model. It all depends on where you are; here on earth such additional data inputs could be taken from a magnetometer, and also an altimeter. It has been shown that adding the magnetometer data alone can reduce that 150 meter error to only 5 meters. The study is a few years old, but we expect it to be about right, as progress with MEMS technology has not improved all that much.

Want to see how good or bad inertial navigation is in real life? A fantastic device for doing all this complicated multi-sensor fusion stuff is the Bosch BNO055, for which Adafruit have helpfully popped on a module. You just might want to brush up on quaternions before you do, mind.

All these measurements will exhibit an error, which will have some particular statistical distribution. One technique to mitigate this error is by using Kalman filtering, which is used heavily by inertial navigation systems. A Kalman filter enables a better understanding of the unknowns in a model, and essentially adjusts itself over time, to allow more influence from measurement points with the least uncertainty. The result is hopefully a better positional fix and an idea of which way you’re currently pointing. But, you still can’t get away with it for long, the error is still there, and it will still accumulate given enough time. Current research seems to suggest an error figure of about 5% of total distance travelled, best case. Longer term, sub-meter inertial navigation is the goal, and we aren’t there yet.

MEMS Sensors: Sources of Error

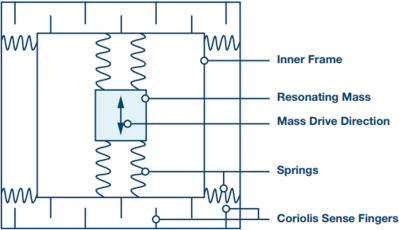
The MEMS gyro is a dynamic device, in that it consists of a tiny vibrating structure that detects angular rotation rate by leveraging the coriolis effect. A mechanical shift is induced orthogonal to the vibration direction, which is sensed as a small change in capacitance.

Gyro sensors typically exhibit two main kinds of error; a rate bias and an angle random walk error, the latter is due to thermo-mechanical white noise and flicker noise in the signal chain electronics. The random walk error grows with time, which is what contributes mostly to the overall absolute orientation error. The rate bias however can be measured long-term and largely cancelled out. There are some other so-called calibration effects that affect stability and will also contribute error terms that are harder to compensate for.

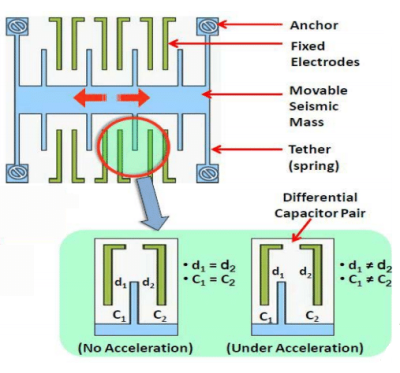
The MEMS accelerometer has a more static structure, and is essentially a sprung element which deflects in one axis to due to acceleration. This mechanical shift is also picked up as a tiny change in capacitance. Again, we have the same two main sources of error; acceleration bias error and velocity random walk error. The bias error now is more complicated, because on this planet we have gravity, and in order to cancel out the bias error, we need to know the orientation of the sensor. Luckily with a multi-sensor fusion system, the orientation can be measured and this bias can be compensated. The velocity random walk error is again due to thermo-mechanical effects and accumulates with time. Also, as with the gyro, there are additional error factors that add to problem.

Other sensors used for inertial navigation systems will all have their own sources of error, and add to the complexity of the problem. There are optical gyros available, for example the ring laser gyro, and more esoteric devices, but these are not necessarily easy to make really small. For example, the ring laser gyro is less accurate the smaller you make it due to the limit in the maximum beam path length. This is why current research is taking a very different approach to this type of sensing; namely the atom interferometer.

Atom Interferometry

Back in 1924 French physicist Louis de Broglie proposed that matter behaves like a wave, with a wavelength equal to the Planck constant divided by its momentum. This meant that just like light, matter waves can be diffracted and produce interference patterns. In this case matter waves are manipulated with lasers, which leads us into the fun part. Remember though, that unlike light, atoms are massive and such, gravity has an influence, as we shall see.

Most atom interferometer experiments seem to operate similarly, in that they all depend upon a high vacuum pressure vessel, and utilise a magneto-optical trap to cool and slow down a stream of rubidium atoms produced from some source. This device uses six intersecting, circularly polarised laser beams, aimed at the centre of the device, with a pair of anti-Helmholtz coils at the top and bottom.

A Helmholtz coil is configured to generate a uniform magnetic field, using a single pair of coils, with current flowing in the same direction. The anti-Helmholtz coil (aka Maxwell gradient coil) simply flips one of the coils over, to produce a magnetic field gradient, with a field zero at the centre. Exactly what we need to trap those pesky little atoms.

The photons from the containment lasers give the atoms a little kick in momentum, and due to the Zeeman effect, the specially-shaped magnetic field ensures that atoms are more likely to get pushed back towards the optical null in the centre of the trap. On average the atoms in the trap centre slow down enough to reach temperatures of a few micro-kelvin. Which is jolly chilly.

The next bit is where things get a bit freaky. The trap is turned off, and immediately each of the suitably frigid atoms is hit with a specially prepared laser pulse, formed by a pair of opposing lasers, either Raman or Bragg transitions are effected, depending on the properties of the laser pulses. The atoms are forced into a quantum superposition of being both hit and not hit by the pulse. This causes the atoms to change momentum and state. (And not, simultaneously, it’s superposition of states, right?) The atom cloud diverges and depending on the motion of the cell, interferes with itself as it expands out from trap centre.

When a low power laser illuminates the atom cloud, the superposition collapses and the interference pattern is observed on a suitably placed CCD. By decoding this pattern it is possible to infer angular velocity as well as acceleration, with incredible accuracy that will open up new applications both on earth and beyond. NASA are interested for one.  For more detail on atom interferometry, checkout this introduction from Berkeley Physics.

Practicality

All of this is of little use as a navigation device if you can’t get it out of the lab and shrink it down in size, make it reliable and make it cheap. Sounds easy, right? Let’s look at the requirements for an atomic gyroscope: you need a pressure vessel with optically pure windows, usually sapphire, that can maintain a pressure of less than 10^-7 torr with very low contamination. You also need the lasers themselves, with associated filters and control electronics. All of those things can be miniaturized, even down to chip size, but maintaining that vacuum is a big challenge. The usual way to get down to such low vacuum pressure is with a turbomolecular pump, in combination by an ion pump. Making these smaller has proved problematic.

A Passive Pumped Vacuum Package

Now there is a possibility of removing the need for that complex and bulky vacuum system. A team from Sandia National Laboratories and the University of Oklahoma, have developed a technique for achieving the ultra-high vacuum (UHV) needed for inertial guidance atomic gyroscope applications, without the need for turbo pumps, ion pumps or any pumps at all. OK, that last bit isn’t strictly true, as they needed to get the vacuum to the desired level first and the standard techniques were needed for that, but once the initial conditions were achieved, the pressure vessel could be sealed off permanently, and the pumps removed.

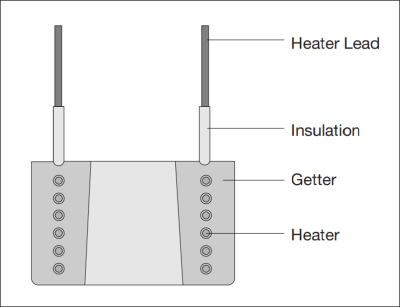
The system relies on chemisorption using sintered porous getters, which are a kind of non-evaporable getter (NEG). These simple passive devices are formed from a sintered porous structure of zirconium powder and other materials, wrapped around an electrical heating element. When manufactured they are exposed to air, forming a passivating coating and protecting them from contamination. When installed in a vacuum chamber, the getter is activated by heating it up during the pump-down process. This diffuses the passivation layer into the bulk of the structure and provides an activated surface ready for adsorbing any contaminants during pump-down and afterwards when the chamber is sealed off. Getters are pretty common in many household vacuum vessel devices, from incandescent light bulbs, to radio valves, but the getters used here are a little bit more specialised than those of old, and capable of grabbing more atoms over a longer period and keep them contained.

The whole point here is that in order to have a small pure group of super cool rubidium atoms to poke with lasers, you first need to not have any other atoms kicking around, getting in the way. Such getters are super important for grabbing rogue atoms and maintaining this purity.

Outgassing is a problem with ultra-high vacuum devices. Contaminant gasses present in the structure of the housing diffuse out into the pressure vessel, contaminating the vacuum. Another related issue is that of permeation from the outside of the vessel. NEG devices work on chemical principles, so any helium that manages to diffuse into the vacuum from outside the enclosure will not react with the getter, and will contaminate the vacuum.  Both of these problems were minimised by careful selection of materials. The frame was made from pure titanium, which had a low hydrogen content, with the windows made from sapphire, which apparently has no measurable helium permeability. These two materials have closely matched thermal expansion coefficients, which helps to maintain the vacuum seal and reduce stress on the structure as the temperature drops.

The team found that once pumped-down and sealed the ‘passively pumped’ vessel could maintain the 10e-9 torr vacuum pressure needed for over 200 days, and that means if all the other components could be successfully miniaturised, there is now a path to producing the first small and therefore portable MOT, and with it an atom interferometer capable of inertial guidance applications. Of course, since the application here is essentially an accelerometer, it can be used as a super-sensitive gravimeter which would be useful for ground surveying for sectors such as oil and mineral exploration as well as for geological research.