Orbital mechanics is a fun subject, as it involves a lot of seemingly empty space that’s nevertheless full of very real forces, all of which must be taken into account lest one’s spacecraft ends up performing a sudden lithobraking maneuver into a planet or other significant collection of matter in said mostly empty space. The primary concern here is that of gravitational pull, and the way it affects one’s trajectory and velocity. With a single planet providing said gravitational pull this is quite straightforward to determine, but add in another body (like the Moon) and things get trickier. Add another big planetary body (or a star like our Sun), and you suddenly got yourself the restricted three-body problem, which has vexed mathematicians and others for centuries.
The three-body problem concerns the initial positions and velocities of three point masses. As they orbit each other and one tries to calculate their trajectories using Newton’s laws of motion and law of universal gravitation (or their later equivalents), the finding is that of a chaotic system, without a closed-form solution. In the context of orbital mechanics involving the Earth, Moon and Sun this is rather annoying, but in 1772 Joseph-Louis Lagrange found a family of solutions in which the three masses form an equilateral triangle at each instant. Together with earlier work by Leonhard Euler led to the discovery of what today are known as Lagrangian (or Lagrange) points.
Having a few spots in an N-body configuration where you can be reasonably certain that your spacecraft won’t suddenly bugger off into weird directions that necessitate position corrections using wasteful thruster activations is definitely a plus. This is why especially space-based observatories such as the James Webb Space Telescope love to hang around in these spots.
Stable and Unstable Stable
Although the definition of Lagrange points often makes it sound like you can put a spacecraft in that location and it’ll remain there forever, it’s essential to remember that ‘stationary’ only makes sense in particular observer’s reference frame. The Moon orbits the Earth, which orbits the Sun, which ultimately orbits the center of the Milky Way, which moves relative to other galaxies. Or it’s just the expansion of space-time which make it appear that the Milky Way moves, but that gets one quickly into the fun corners of theoretical physics.

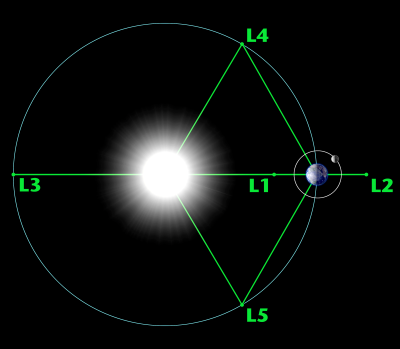
Within the Earth-Sun system, there are five Lagrange points (L1 – L5), of which L2 is currently the home of the James Webb Space Telescope (JWST) and was the home to previous observatories (like the NASA WMAP spacecraft) that benefit from always being in the shadow of the Earth. Similarly, L1 is ideal for any Sun observatory, as like L2 it is located within easy communication distance
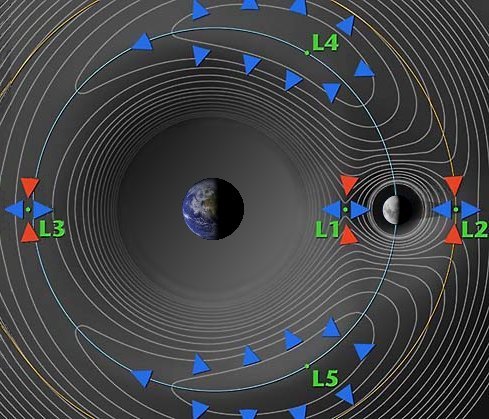
Perhaps shockingly, the L3 point is not very useful to put any observatories or other spacecraft, as the Sun would always block communication with Earth. What L3 has in common with L1 and L2 is that all of these are unstable Lagrange points, requiring course and attitude adjustments approximately every 23 days. This contrasts with L4 and L5, which are the two ‘stable’ points. This can be observed in the above contour plot, where L4 and L5 are on top of ‘hills’ and L1 through L3 are on ‘saddles’ where the potential curves up in one direction and down another.
One way to look at it is that satellites placed in the unstable points have a tendency to ‘wander off’, as they don’t have such a wide region of relatively little variance (contour lines placed far from each other) as L4 and L5 do. While this makes these stable points look amazing, they are not as close to Earth as L1 and L2, and they have a minor complication in the fact that they are already occupied, much like the Earth-Moon L4 and L5 points.
Because of how stable the L4 and L5 points are, the Earth-Moon system ones have found themselves home to the Kordylewski clouds. These are effectively concentrations of dust which were first photographed by Polish astronomer Kazimierz Kordylewski in 1961 and confirmed multiple times since. Although a very faint phenomenon, there are numerous examples of objects caught at these points in e.g. the Sun-Neptune system (Neptune trojans) and the Sun-Mars system (Mars trojans). Even our Earth has picked up a couple over the years, many of them asteroids. Of note that is the Earth’s Moon is not in either of these Lagrange points, having become gravitationally bound as a satellite.
All of which is a long way to say that it’s okay to put spacecraft in L4 and L5 points as long as you don’t mind fragile technology sharing the same region of space as some very large rocks, with an occasional new rocky friend getting drawn into the Lagrange point.
Stuff in Lagrange Points
A quick look at the Wikipedia list of objects at Lagrange points provides a long list past and current natural and artificial objects at these locations, across a variety of system. Sticking to just the things that we humans have built and sent into the Final Frontier, we can see that only the Sun-Earth and Earth-Moon systems have so far seen their Lagrange points collect more than space rocks and dust.
Starting with Sun-Earth, the L1 point has:
- Solar and Heliospheric Observatory (SOHO, ESA)
- Advanced Composition Explorer (ACE, NASA)
- Global Geospace Science WIND (GGS, NASA)
- Deep Space Climate Observatory (DSCOVR, NOAA)
- Aditya-L1 (ISRO)
These will be joined if things go well by IMAP in 2025 along with SWFO-L1, NEO Surveyor in 2027. These spacecraft mostly image the Sun, monitor solar wind, image the Earth and its weather patterns, for which this L1 point is rather excellent. Of note here is that strictly taken most of these do not simply linger at the L1 point, but rather follow a Lissajous orbit around said Lagrange point. This particular orbital trajectory was designed to compensate for the instability of the L1-3 points and minimize the need for course corrections.
Moving on, the Sun-Earth L2 point is also rather busy:
- Gaia space observatory (ESA)
- Spektr-RG astrophysics observatory (Russian-German)
- James Webb Space Telescope (JWST, NASA, ESA, CSA)
- Euclid space telescope (ESA)
- Chang’e 6 orbiter (CNSA)
Many of the planned spacecraft that should be joining the L2 point are also observatories for a wide range of missions, ranging from general observations in a wide range of spectra to exoplanet and comet hunting.
Despite the distance and hazards of the Sun-Earth L4 and L5 points, these host the Solar TErrestrial RElations Observatory (STEREO) A and B solar observation spacecraft. The OSIRIS-REx and Hayabusa 2 spacecraft have passed through or near one of these points during their missions. The only spacecraft planned to be positioned at one of these points is ESA’s Vigil, which is scheduled to launch by 2031 and will be at L5.
Only the Moon’s L2 point currently has a number of spacecraft crowding about, with NASA’s THEMIS satellites going through their extended mission observations, alongside the Chinese relay satellite Queqiao-2 which supported the Chang’e 6 sample retrieval mission.
In terms of upcoming spacecraft to join the sparse Moon Lagrange crowd, the Exploration Gateway Platform was a Boeing-proposed lunar space station, but it was discarded in favor of the Lunar Gateway which will be placed in a polar near-rectilinear halo orbit (NRHO) with an orbital period of about 7 days. This means that this space station will cover more of the Moon’s orbit rather than remain stationary. It is intended to be launched in 2027, as part of the NASA Artemis program.
Orbital Mechanics Fun
The best part of orbits is that you have so many to pick from, allowing you to not only pick the ideal spot to idle at if that’s the mission profile, but also to transition between them such as when traveling from the Earth to the Moon with e.g. a trans-lunar injection (TLI) maneuver. This involves a low Earth orbit (LEO) which transitions into a powered, high eccentric orbit which approaches the Moon’s gravitational sphere of influence.
Within this and low-energy transfer alternatives the restricted three-body problem continuously applies, meaning that the calculations for such a transfer have to account for as many variables as possible, while in the knowledge that there is no perfect solution. With our current knowledge level we can only bask in the predictable peace and quiet that are the Lagrange points, if moving away from all those nasty gravity wells like the Voyager spacecraft did is not an option.
















Wonderful article. Thank you!
Surely, the reference to buggery should be reserved for the Lagrange point around Uranus?
that is only applicable to klingons
_:(´ཀ`」 ∠):
In case you did not get the memo, The Astronomical Society together with Nat Geo and the Minor Planets Bureau have deprecated that noxious name. The new name? Urectum.
While the two NASA THEMIS satellites repurposed for the ARTEMIS mission made use of the Earth-Moon L1 and L2 points as part of their transfer orbits from Earth orbit to lunar orbit back in 2010, both satellites, now known as the ARTEMIS satellites, are in more traditional Moon-centered orbits.
The other three THEMIS satellites remain in Earth orbit, continuing to collect science data.
Note that this ARTEMIS mission is independent of the NASA human exploration office’s Artemis program, although each complements the other’s objectives and goals.
Source: I’m one of the science instrument leads on the THEMIS/ARTEMIS mission.
Thank you very much for those details, John. While writing the article I found that Wikipedia is pretty outdated when it comes to the current status (and location/orbit) of spacecraft in Lagrange points, which got me pretty deep in the weeds on some missions. I very much appreciate the input from someone with first-hand knowledge.
For reference, here’s the DOI for one of the articles written about the ARTEMIS mission design, including the use of various Earth-Sun and Earth-Moon Lagrange points as a key part of the low delta-V transfer from Earth to lunar orbit:
Space Science Reviews, Volume 165, Issue 1-4, pp. 27-57
https://ui.adsabs.harvard.edu/link_gateway/2011SSRv..165…27S/doi:10.1007/s11214-012-9869-1
Let me ask a question,
If there is no stuff in L3 (sun-earth), how we know that there are any object, e.g small asteroids, or small planet hide or trapped in L3? Because the sun can eclipse any object in L3.
Because both STEREO A and B only monitor the sun.
If you look at the contour lines, L3 is not as stable as L4 or L5, so if there were any objects there they would need to expend energy to remain there hidden. Probably a seed idea in there somewhere for for a “Iron Sky III” film, but there is no secret small planet.
Correction “Iron Sky IV” film, looks like there might, or might not, be an Iron Sky III: The Ark film – there is a trailer.
STEREO B is defunct quite some time..
STEREO B is defunct tor quite some time though..
that’s where the teapot is
It’s science like this that proves Moon is likely to exist. I wish it was more widespread so people on Facebook would not post anti-scientific bs.
Do people say that the moon doesn’t exist? I have heard of people claiming that we never landed on the moon, or that the moon is flat, but I don’t think I’ve heard people saying that it isn’t there. Can you point me to an example or two?
Never waste your any time from your life trying to convince someone with a strong belief or faith that something is true to change their mind. Before facebook they existed in small isolated pockets around the world, now they have been herded into large groups and amplify their misconceptions. It is a total waste of your life. You may as well try to teach a dog how to solve three dimensional partial differential complex equations, although maybe with a really really smart dog, you might have some chance, but you would have none with a clump of idiots.
So, maybe someone here can answer a question. Why are L4 and L5 points always in one plane? The gravitational attraction between Earth and Moon is equal at a series of points between them that form a circle passing through both L4 and L5. In other words, why couldn’t a satelite be placed in a stable orbit perpendicular to the line between the Earth and Moon that passes through L4 and L5, rather than be stationary at either point? If so, there is significantly more orbital space available. Similarly, orbiting L2 outside of the Moon’s shadow would be far more useful than being stationary there.
(I might be completely wrong, but this is how I see it)
While the image is stationary, you’ll have to think about it that the whole thing is actually rotating as the moon orbits the earth. So, the L4/L5 points are also orbiting, and at those specific points, the attraction from the earth, attraction from the moon and your required orbital velocity change match exactly. By moving anywhere on the line you suggest, your orbital velocity changes, and it no longer matches up with the attraction from earth/moon.
Thank you. The addition of rotation makes sense. Speed gained in the retrograde part of the orbit might not exactly match speed lost in the prograde part if the path isn’t perfect. So, the circular orbits as described wouldn’t be stable but still might be useful low-energy orbits.
“In other words, why couldn’t a satelite be placed in a stable orbit perpendicular to the line between the Earth and Moon that passes through L4 and L5”
Imagine yourself at L1, which is by far the easiest to understand. If you’re above the plane of the Earth/Moon, gravity between the Earth and the Moon isn’t balanced. They’re both below you. You’re going to be pulled down. Reverse is true if you’re below the plane.
Obviously, you can guess as to what that leads to: it’s just basic simple harmonic motion. You’ll bounce up and down around the Lagrange point.
That’s basically the idea behind a Lagrange halo orbit (although what I just gave is still an unstable situation). Your “orbiting L2 outside the Moon’s shadow?” Yeah. That’s Gateway’s NRHO orbit.
However you’re not actually orbiting the Lagrange points in many of them, it’s just a family of orbits associated with it. The actual dynamics of the out-of-plane motion around Lagrange points is exceptionally complicated.
https://gereshes.com/2019/11/04/periodic-orbits-around-lagrange-points/
Wow. Way more complicated than I had thought. Very interesting, but they really should have controls on the gifs so you can stop them. I recommend skipping to the “Interactives” links at the bottom.
I should’ve also clarified: one of the mistakes people make with Lagrange points (using, say, the Sun/Earth system) is thinking that L1 is where the force of gravity from the Sun is equal to the force of gravity from the Earth, because that’s kinda what it looks like.
That’s not the case: that point happens way closer to the Sun than L1, and you can’t orbit there – there’s no centripetal force to keep you in an orbit. At L1, the Sun’s gravity still dominates over the Earth, because you’re still orbiting the system’s barycenter, so there needs to be a centripetal force pointing towards the Sun.
What’s balanced to zero at the Earth/Sun Lagrange points are the sum of the gravitational forces minus the centripetal force corresponding to an orbital period of 1 year. That’s how L2 works – normally you’d be orbiting slower than the Earth when you’re farther away from the Sun, but the extra gravity from the Earth being so close speeds you up exactly the right amount.
Proper N-body simulations have really only become computationally tractable in the past 20-30 years or so.
One other thing to factor in is that the L4 and L5 due to their increased stability will have a lot more objects floating/orbiting within them so each time your craft went through them it would be like sprinting through a shooting gallery, they may not survived passing through.
The orbits associated with L4/L5 don’t really go “through” them, though – in fact they tend to wander like, stupidly far away from them because the potential’s so shallow there. Some of the orbits associated with L4/L5 are basically common orbits hopping between the two! This is basically how the interplanetary superhighway orbits work – the potential’s so shallow near Lagrange points that you just orbit near them, and eventually the arrangement of the Solar System gives you a transit between whatever Lagrange point you’re at to the destination you want.
Remember, those are equipotential contours up there – if you look at the spacing between two contours near L4/L5, they’re absurdly larger than the ones near L1/L2. (Similarly with L3 – even though the overall potential shape is similar the size of the orbit distribution near L3 is much larger).
It’s still a tough place to be from an orbital mechanics standpoint because since the potential so shallow and the orbits are large, tons of random small objects will pass through.
“sudden lithobraking maneuver”
That had me laughing.
Fascinating article! Thank you, Maya.
Great article!
Great article, Maya! Good visuals too. Is the header image by Joe Kim as usual? Love the perspective!
Thank you, Dave! Yes, the header image is another amazing work of art by Joe Kim :)
Honest, I think we should be flooding the L1 point with a heavier than air substance that will reflect IR. Earth has too much heat and we need to balance it out before too much goes wrong… and it is going wrong at an increasingly speedy pace. The key is that the substance needs to be safe to enter Earth’s atmosphere because solar wind will blow it back to us.
Go ahead: calculate how much material we need to place there to reduce insolation by, say, ten percent. Then figure out how much mass we’ll pay in rocket propellant to get it there. It’s a staggering figure (many megatons).
Maybe it’s worth it to spend a substantial fraction of the world’s GDP on cooling off the planet a bit this way.
Maybe it’s worth spending those millions of peoples’ lives to do so.
Maybe it would do the ‘economy’ good to employ all those people in pursuit of that goal.
But maybe, just maybe, there are more sensible ways of doing it than lobbing megatons of stuff to L1.
So to be clear, in my opinion you’re not wrong, it’s insane: – but reducing insolation by 10% would kill us. It’s not linear in the slightest bit (it’s the Stefan-Boltzmann relation) but for small changes (up to ~10% or so) it’s about 1 deg C per percent. An 8 deg C drop in average global temperature would Be Bad. Realistically you only need 1-2%.
People have actually calculated rough cost estimates for this kind of thing, because it’s always smart to do that so people don’t think you’re summarily dismissing them, although in my opinion these estimates are always waay too low: generally it’s in the tens of trillions range, and they’ve got insane assumptions like millions of gram-scale satellites.
Weird, I just read about Lagrange points from a fiction book, where a group of oxford scientists develop an AI which helps them develop new physics and they go on to save the world, a bit long and geeky but was quite a nice read especially near the end where they develop the space travel stuff.
Was one of those scientists named “Mary Sue”?
B^)
https://en.wikipedia.org/wiki/Mary_Sue
Slightly tangential but there’s a lovely youTube about the Dr Who episode The Wheel in Space using real science, including an unpicking of the location of ‘the wheel’ based on Lagrange Points. It’s super geeky fun.
https://www.youtube.com/watch?v=KQfrfOdpOEU&ab_channel=Dalek63%E2%80%A288