When faced with an FPGA, some people might use it to visualize the Mandelbrot set. Others might use it to make CPUs. But what happens if you combine the two? [Michael Kohn] shows us what happens with his RISC-V CPU with an instruction specially made for computing the Mandelbrot set.
[Michael] takes us through the unusual process of turning his 8008 into a RISC-V CPU. Re-using bits of logic here and replacing other logic there leaves him with a functional RISC-V core. Not finished, [Michael] takes it upon himself to also create a custom instruction just for computing a point for the Mandelbrot set, accelerating the demo from twenty-three seconds to merely one!
Still not finished, [Michael] also creates an implementation of the long gone F100-L CPU, once again with added Mandelbrot set flair, simultaneously with the RISC-V project. Finally, he ports his “Java Grinder” Java bytecode compiler to both RISC-V and the F100-L, because Java runs on 1 Billion devicesTM.
Continue reading “Compute The Mandelbrot Set With A Custom RISC-V CPU”
for which the function 
does not diverge.” Even if you don’t understand the mathematics behind it, you’ve likely seen the complicated fractal images generated by zooming in on the border of the Mandelbrot set. [Scott Williamson] not only got this set rendering on an Atari, 
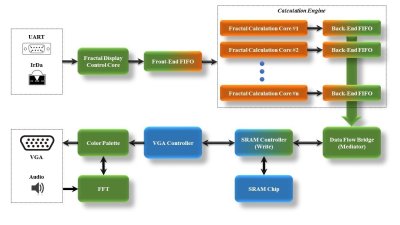On the FPGA, a custom calculation engine, running at up to 150 MHz, does the math to generate the fractal. A Fast Fourier transform decomposes the audio input into frequencies, which are used to control the colors of the output image.
