Hackaday reader [nats.fr] wrote in with some code from a project that resizes a video stream on the fly using an FPGA. Doing this right means undoing whatever gamma correction has been applied to the original stream, resizing, and then re-applying the gamma. Making life simpler, [nats.fr] settled on a gamma of two, which means taking a bunch of square roots, which isn’t fast on an FPGA.
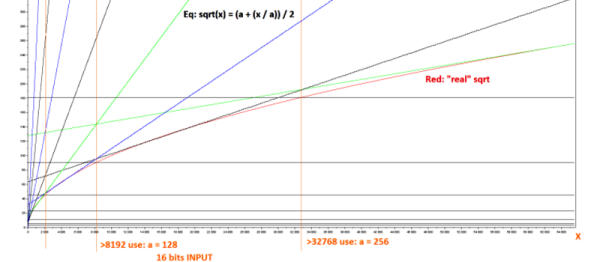
[nats]’s algorithm is pretty neat: it uses a first-stage lookup to figure out in which broad range the value lies, and then one step of Hero’s algorithm to refine from there. (We think this is equivalent to saying he does a piecewise linear interpolation, but we’re not 100% sure.) Anyway, it works decently.
Of course, when you start looking into the abyss that is special function calculation, you risk falling in. Wikipedia lists more methods of calculating square roots than we have fingers. One of them, CORDIC, avoids even using multiplication by resorting to clever bitshifts and a lookup table. Our go-to in these type of situations, Chebyshev polynomial approximation, didn’t even make the cut. (Although we suspect it would be a contender in the gamma=1.8 or gamma=2.2 cases, especially if combined with range-reduction in a first stage like [nats.fr] does.)
So what’s the best/fastest approximation for sqrt(x) for 16-bit integers on an FPGA? [nats.fr] is using a Spartan 6, so you can use a multiplier, but division is probably best avoided. What about arbitrary, possibly fractional, roots?