The Deep Magic Of 3D Graphics Perspective

September 29, 2026 by Bryan Cockfield 3 Comments

Many of us of a certain age will have had their first true, good 3D video game experience with Super Mario 64. Unlike previous 3D games, the camera was an object controllable by the player, rather than a first-person-ony mode or one where the game tries to guess the best placement for the camera. We might take this mechanic for granted today, but 3D was a new technology at the time that took experimentation before settling on the norms we have today. From a programming perspective, 3D graphics can be a bit of a head-scratcher but [Gabriel] shows that perspective and the camera can be as simple as a few lines of math.

When starting out as a programmer, [Gabriel] used various tools that provided a camera somewhat automatically. But after reaching the limits of these types of frameworks, the next step is to learn how that works from scratch. It turns out that it’s a bit of matrix math, with values for foreground and background clipping planes as well as aspect, field of view, and position. This basically replicates a trapezoidal prism which can be thought of as a viewer looking at a scene from the perspective of a camera. To provide the depth effect, the X and Y coordinates are divided by the Z coordinate within this matrix system, making far-away objects smaller and generating the 3D effect.

On [Gabriel]’s site which explains this method, there are a few sliders in several examples that demonstrate how changing values of each of these variables changes the perspective and the object being displayed. For a math lesson it is very interactive and helps intuit these concepts. Cameras aside, the generation of 3D objects has its own unique set of math equations to learn about that are “equally” interesting.

Size (and Units) Really Do Matter

January 23, 2026 by Al Williams 94 Comments

We miss the slide rule. It isn’t so much that we liked getting an inexact answer using a physical moving object. But to successfully use a slide rule, you need to be able to roughly estimate the order of magnitude of your result. The slide rule’s computation of 2.2 divided by 8 is the same as it is for 22/8 or 220/0.08. You have to interpret the answer based on your sense of where the true answer lies. If you’ve ever had some kid at a fast food place enter the wrong numbers into a register and then hand you a ridiculous amount of change, you know what we mean.

Recent press reports highlighted a paper from Nvidia that claimed a data center consuming a gigawatt of power could require half a million tons of copper. If you aren’t an expert on datacenter power distribution and copper, you could take that number at face value. But as [Adam Button] reports, you should probably be suspicious of this number. It is almost certainly a typo. We wouldn’t be surprised if you click on the link and find it fixed, but it caused a big news splash before anyone noticed.

Thought Process

Best estimates of the total copper on the entire planet are about 6.3 billion metric tons. We’ve actually only found a fraction of that and mined even less. Of the 700 million metric tons of copper we actually have in circulation, there is a demand for about 28 million tons a year (some of which is met with recycling, so even less new copper is produced annually).

Simple math tells us that a single data center could, in a year, consume 1.7% of the global copper output. While that could be true, it seems suspicious on its face.

Digging further in, you’ll find the paper mentions 200kg per megawatt. So a gigawatt should be 200,000kg, which is, actually, only 200 metric tons. That’s a far cry from 500,000 tons. We suspect they were rounding up from the 440,000 pounds in 200 metric tons to “up to a half a million pounds,” and then flipped pounds to tons.

Continue reading “Size (and Units) Really Do Matter” →

An Introduction To Analog Filtering

December 4, 2025 by Bryan Cockfield 8 Comments

One of the major difficulties in studying electricity, especially when compared to many other physical phenomena, is that it cannot be observed directly by human senses. We can manipulate it to perform various tasks and see its effects indirectly, like the ionized channels formed during lightning strikes or the resistive heating of objects, but its underlying behavior is largely hidden from view. Even mathematical descriptions can quickly become complex and counter-intuitive, obscured behind layers of math and theory. Still, [lcamtuf] has made some strides in demystifying aspects of electricity in this introduction to analog filters.

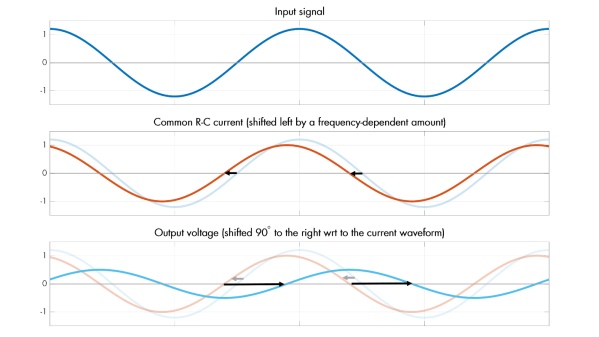
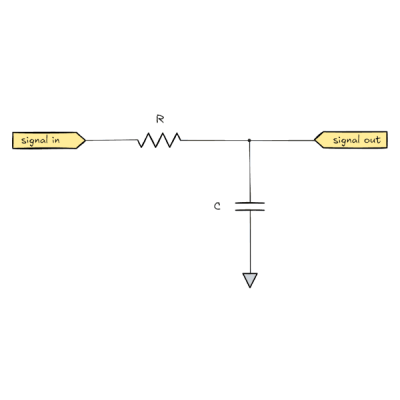The discussion on analog filters looks at a few straightforward examples first. Starting with an resistor-capacitor (RC) filter, [lcamtuf] explains it by breaking its behavior down into steps of how the circuit behaves over time. Starting with a DC source and no load, and then removing the resistor to show just the behavior of a capacitor, shows the basics of this circuit from various perspectives. From there it moves into how it behaves when exposed to a sine wave instead of a DC source, which is key to understanding its behavior in arbitrary analog environments such as those involved in audio applications.

There’s some math underlying all of these explanations, of course, but it’s not overwhelming like a third-year electrical engineering course might be. For anyone looking to get into signal processing or even just building a really nice set of speakers for their home theater, this is an excellent primer. We’ve seen some other demonstrations of filtering data as well, like this one which demonstrates basic filtering using a microcontroller.

How To Use That Slide Rule

November 21, 2025 by Al Williams 31 Comments

You have that slide rule in the back of the closet. Maybe it was from your college days. Maybe it was your Dad’s. Honestly. Do you know how to use it? Really? All the scales? That’s what we thought. [Amen Zwa, Esq.] not only tells you how slide rules came about, but also how to use many of the common scales. You can also see his collection and notes on being a casual slide rule collector and even a few maintenance tips.

The idea behind these computing devices is devilishly simple. It is well known that you can reduce a multiplication operation to addition if you have a table of logarithms. You simply take the log of both operands and add them. Then you do a reverse lookup in the table to get the answer.

Continue reading “How To Use That Slide Rule” →

The Sanskrit Square Root Algorithm

November 10, 2025 by Al Williams 13 Comments

Years ago, no math education was complete without understanding how to compute a square root. Today, you are probably just reaching for a calculator, or if you are writing a program, you’ll probably just guess and iterate. [MindYourDecisions] was curious how people did square roots before they had such aids. Don’t remember? Never learned? Watch the video below and learn a new skill.

The process is straightforward, but if you are a product of a traditional math education, you might find his terminology a bit confusing. He will refer to something like 18b meaning “a three-digit number where the last digit is b,” not “18 times b,” as you might expect.

Continue reading “The Sanskrit Square Root Algorithm” →

Teaching Math With 3D Printers

October 25, 2025 by Al Williams 10 Comments

We’ve often thought that 3D printers make excellent school projects. No matter what a student’s interests are: art, software, electronics, robotics, chemistry, or physics, there’s something for everyone. A recent blog post from [Prusa Research] shows how Johannes Kepler University is using 3D printing to teach math. You can see a video with Professor [Zsolt Lavicza] explaining their vision below.

Instead of relying on abstract 3D shapes projected on a 2D screen, GeoGebra, educational math software, creates shapes that you can produce on a 3D printer. Students can physically handle and observe these shapes in the real world instead of on a flat screen.

One example of how the 3D printer finds use in a math class is producing “Genius Square,” a multilevel tic-tac-toe game. You can find the model for that and other designs used in the classes, on Printables. Some prints are like puzzles where students assemble shapes from pieces.

Putting 3D printers in school isn’t a new idea, of course. However, machines have become much simpler to use in recent years, so maybe the time is now. If you can’t find money for printers in school, you can always teach robotics using some low-tech methods.

Continue reading “Teaching Math With 3D Printers” →

8 Bit Mechanical Computer Built From Knex

July 20, 2025 by Bryan Cockfield 24 Comments

Long before electricity was a common household utility, humanity had been building machines to do many tasks that we’d now just strap a motor or set of batteries onto and think nothing of it. Transportation, manufacturing, agriculture, and essentially everything had non-electric analogs, and perhaps surprisingly, there were mechanical computers as well. Electronics-based computers are far superior in essentially every way, but the aesthetics of a mechanical computer are still unmatched, like this 8-bit machine built from K’nex.

Continue reading “8 Bit Mechanical Computer Built From Knex” →