Weigh Your Car With Paper

September 30, 2020 by Brian McEvoy 23 Comments

Sometimes a problem is more important than its solution. Humans love to solve mysteries and answer questions, but the most rewarding issues are the ones we find ourselves. Take [Surjan Singh], who wanted to see if he could calculate the weight of his Saab 96. Funny enough, he doesn’t have an automobile scale in his garage, so he had to concoct a workaround method. His solution is to multiply the pressure in his tires with their contact patch. Read on before you decide this is an imperfect idea.

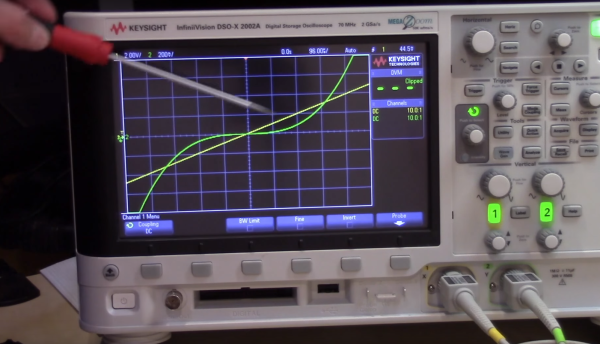
He measures his tires with a quality gauge for the highest accuracy and pressurizes them equally. Our favorite part is how he measures the contact patch by sliding a couple of paper pieces from the sides until they stop and then measures the distance between them. He quickly realizes that the treads didn’t contact the floor evenly, so he measures them to get a better idea of the true contact area. Once he is satisfied, he performs his algebra and records the results, then drives to some public scales and has to pay for a weigh. His calculations are close, but he admits this could be an imprecise method due to an n-of-one, and that he didn’t account for the stiffness of the tire walls.

This was a fun thought experiment with real-world verification. If you’re one of those people who treats brainstorming like an Olympic sport, then you may enjoy the gedankenexperiment that is fractals.

Mathematical Proof The Eagle In The USPS Logo Is FAST!

April 18, 2020 by Daniel Bogdanoff 33 Comments

The logo for the United States Postal Service is a mean-looking eagle. But a true fluid dynamics geek might look at it and realize that eagle is moving so fast it’s causing a shock wave. But just how fast is it moving? [Andrew Higgins] asked and answered this question, posting his analysis of the logo’s supersonic travel. He claims it’s Mach 4.9, but, how do we know? Science!

It turns out if something is going fast enough, you can tell just how fast with a simple picture! We’ve all seen pictures of jets breaking the sound barrier, this gives us information about the jet’s speed.

How does it work?

Think about it like this: sound moves at roughly 330 m/s on Earth at sea level. If an object moves through air at that velocity, the air disturbances are transmitted as sound waves. If it’s moving faster than sound, those waves get distributed downstream, behind the moving object. The distance of these waves behind the moving object is dependent on the object’s speed.

This creates a line of these interactions known as a “Mach line.” Find the angle difference of the Mach line and the direction of travel and you have the “Mach angle” (denoted by α or µ).

There is a simple formula for determining the speed of an object using the Mach angle, the speed of sound (a), and an object’s velocity (v): sin(µ) = a / v. The ratio of v to a is known as the Mach number, (M). If an object is going exactly the speed of sound, it’s going Mach 1 (because v = a).

Since Mach number (M) is v / a, we can plug it into the formula from above as 1 / M and use [Andrew]’s calculation shown in the image at the top of the article for a Mach angle (µ) of ~11.7°:

$\bf \sin ( \mu ) = \frac{1}{M} \\ \\ M = \frac{1}{\sin(\mu)} \\ \\ M = \frac{1}{\sin(11.7)} \\ \\ M = \frac{1}{0.202787295357} \\ \\ M = 4.9312753949380048$

The real question is, did the USPS chose Mach 4.93 as a hint to some secret government postal project? Or, was it simply a 1993 logo designer’s attempt to “capture the ethos of a modern era which continues today”?

How Smart Are AI Chips, Really?

November 4, 2019 by Maya Posch 52 Comments

The best part about the term “Artificial Intelligence” is that nobody can really tell you what it exactly means. The main reason for this stems from the term “intelligence”, with definitions ranging from the ability to practice logical reasoning to the ability to perform cognitive tasks or dream up symphonies. When it comes to human intelligence, properties such as self-awareness, complex cognitive feats, and the ability to plan and motivate oneself are generally considered to be defining features. But frankly, what is and isn’t “intelligence” is open to debate.

What isn’t open to debate is that AI is a marketing goldmine. The vagueness has allowed for marketing departments around the world to go all AI-happy, declaring that their product is AI-enabled and insisting that their speech assistant responds ‘intelligently’ to one’s queries. One might begin to believe that we’re on the cusp of a fantastic future inhabited by androids and strong AIs attending to our every whim.

In this article we’ll be looking at the reality behind these claims and ponder humanity’s progress towards becoming a Type I civilization. But this is Hackaday, so we’re also going to dig into the guts of some AI chips, including the Kendryte K210 and see how the hardware of today fits into our Glorious Future. Continue reading “How Smart Are AI Chips, Really?” →

Solve 2D Math Equations Colorfully

March 26, 2018 by Al Williams 13 Comments

Electronics can be seen as really just an application of physics, and you could in turn argue that physics is the application of math to the real world. Unfortunately, the way most of us were taught math was far from intuitive. Luckily, the Internet is full of amazing texts and videos that can help you get a better understanding for the “why” behind complex math topics. Case in point? [3Blue1Brown] has a video showing how to solve 2D equations using colors. If you watch enough, you’ll realize that the colors are just a clever way to represent vectors and, in fact, the method would apply to complex numbers.

Honestly, we don’t think you’d ever solve equations like this by hand — at least not with the colors. But the intuitive feel this video can give you for how things work is very valuable. In addition, if you were trying to implement an algorithm in software this would be tailor-made for it, although you wouldn’t really use colors there either we suppose.

Continue reading “Solve 2D Math Equations Colorfully” →

Make Math Real With This Analog Multiplier Primer

June 19, 2016 by Dan Maloney 11 Comments

Remember learning all about functions in algebra? Neither do we. Oh sure, most of us remember linear plots and the magic of understanding y=mx+b for the first time. But a lot of us managed to slide by with only a tenuous grasp of more complex functions like exponentials and conic sections. Luckily the functionally challenged among us can bolster their understanding with this demonstration using analog multipliers and op amps.

[devttys0]’s video tutorial is a great primer on analog multipliers and their many uses. Starting with a simple example that multiplies two input voltages together, he goes on to show circuits that output both the square and the cube of an input voltage. Seeing the output waveform of the cube of a ramped input voltage was what nailed the concept for us and transported us back to those seemingly wasted hours in algebra class many years ago. Further refinements by the addition of an op amp yield a circuit that outputs the square root of an input voltage, and eventually lead to a voltage controlled resistor that can attenuate an input signal depending on its voltage. Pretty powerful stuff for just a few chips.

The chip behind [devttys0]’s primer is the Analog Devices AD633, a pretty handy chip to have around. For more on this chip, check out [Bil Herd]’s post on analog computing.

Continue reading “Make Math Real With This Analog Multiplier Primer” →

Beyond Control: Maths Of A Control System

December 24, 2015 by Brandon Dunson 28 Comments

Control systems are all around us, and understanding them is going to make you much better at hardware design. In the last article — Beyond Control: The Basics of Control Systems — we looked at an overview of what a control systems are in general with the example: “everything in between water and time is a control system”. We also observed control systems in nature, where I described my keen ability to fill a glass of water without catastrophic results. That discussion involved the basic concept of a block diagram (without maths) and we expanded that a bit to see what our satellite dish example would look like (still without maths).

I promised some big ugly maths in this article, and we’ll get to that in a bit, never you fear. First let’s have a look at how some basic elements: resistors, inductors, and capacitors are defined in the time domain. Don’t let these first few definitions turn you off. No matter how you feel about calculus, you don’t necessarily need to fully understand each equation. What’s more important is how the equations themselves combine to solve the circuit. Also important is that I will do everything possible to get out of doing difficult math. So stick with me through the article and you’ll learn that agony-saving trick for yourself!

A quick recap on transfer functions before we get going might be beneficial. A control system is used to define electromechanical behavior. For example: our satellite dish (from the previous article) at some point will need to be moved from one position to another position and as control engineers it is our job to determine just how this action will take place. I’m not talking about setting the mood for the big emotional robotic rotation, more like: not damaging the equipment or any people that might be nearby when moving the dish. For many reasons the dish would need to be moved with extreme care and in a very precise manner. The control system is the mathematical definition of that movement. Often the maths of the definition are nasty differential equations, (remember I’m avoiding any math that can be avoided, right?) so, instead of using differential equations to define the system, the transfer function will define the system with algebra, relating the output of the system to the input.

Continue reading “Beyond Control: Maths Of A Control System” →