slide rule

21 Articles

Sliderule Simulator Teaches You How To Do Calculations The Old Fashioned Way

February 18, 2026 by 18 Comments

Ever wanted to know how engineers made their calculations before digital calculators were on every workbench? [Richard Carpenter] and [Robert Wolf] have just the thing—a sliderule simulator that can teach you how to do a whole bunch of complex calculations the old fashioned way!

The simulator is a digital recreation of the Hemmi/Post 1460 Versalog slide rule. This was a particularly capable tool that was sold from 1951 to 1975 and is widely regarded as one of the best slide rules ever made. It can do all kinds of useful calculations for you just by sliding the scales and the cursor appropriately, from square roots to trigonometry to exponents and even multi-stage multiplication and divisions.

You can try the simulator yourself in a full-screen window here. It’s written in JavaScript and runs entirely in the browser. If you’ve never used a slide rule before, you might be lost as you drag the center slide and cursor around. Fear not, though. The simulator actually shows you how to use it. You can tap in an equation, and the simulator will both spit out a list of instructions to perform the calculation and animate it on the slide rule itself. There are even a list of “lessons” and “tests” that will teach you how to use the device and see if you’ve got the techniques down pat. It’s the sort of educational tool that would have been a great boon to budding engineers in the mid-20th century. With that said, most of them managed to figure it out with the paper manuals on their own, anyway.

We’ve featured other guides on how to use this beautiful, if archaic calculation technology, too. We love to see this sort of thing, so don’t hesitate to notify the tipsline if you’ve found a way to bring the slide rule back to relevance in the modern era!

Thanks to [Stephen Walters] for the tip!

Retrotechtacular: Learning The Slide Rule The New Old Fashioned Way

December 2, 2025 by 14 Comments

Learning something on YouTube seems kind of modern. But if you are watching a 1957 instructional film about slide rules, it also seems old-fashioned. But Encyclopædia Britannica has a complete 30-minute training film, which, what it lacks in glitz, it makes up for in mathematical rigor.

We appreciated that it started out talking about numbers and significant figures instead of jumping right into the slide rule. One thing about the slide rule is that you have to sort of understand roughly what the answer is. So, on a rule, 2×3, 20×30, 20×3, and 0.2×300 are all the same operation.

You don’t actually get to the slide rule part for about seven minutes, but it is a good idea to watch the introductory part. The lecturer, [Dr. Havery E. White] shows a fifty-cent plastic rule and some larger ones, including a classroom demonstration model. We were a bit surprised that the prestigious Britannica wouldn’t have a bit better production values, but it is clear. Perhaps we are just spoiled by modern productions.

We love our slide rules. Maybe we are ready for the collapse of civilization and the need for advanced math with no computers. If you prefer reading something more modern, try this post. Our favorites, though, are the cylindrical ones that work the same, but have more digits.

Continue reading “Retrotechtacular: Learning The Slide Rule The New Old Fashioned Way” →

How To Use That Slide Rule

November 21, 2025 by 30 Comments

You have that slide rule in the back of the closet. Maybe it was from your college days. Maybe it was your Dad’s. Honestly. Do you know how to use it? Really? All the scales? That’s what we thought. [Amen Zwa, Esq.] not only tells you how slide rules came about, but also how to use many of the common scales. You can also see his collection and notes on being a casual slide rule collector and even a few maintenance tips.

The idea behind these computing devices is devilishly simple. It is well known that you can reduce a multiplication operation to addition if you have a table of logarithms. You simply take the log of both operands and add them. Then you do a reverse lookup in the table to get the answer.

Continue reading “How To Use That Slide Rule” →

Slide Rule By Helix

June 4, 2025 by No comments

It is no secret that we like slide rules around the Hackaday bunker, and among our favorites are the cylindrical slide rules. [Chris Staecker] likes them, too, and recently even 3D printed a version. But spurred by comments on his video, he decided to try something that might be unique: a helical slide rule. You can see how it works in the video below.

With a conventional slide rule, the scale is rotated around a cylinder so that it is the same length as a much longer linear scale. However, this new slide rule bends the entire rule around a cylinder and allows the slide to move, just like a conventional slide rule. If you have a 3D printer, you can make your own.

Continue reading “Slide Rule By Helix” →

Unwinding An Unusual Slide Rule

May 12, 2025 by 15 Comments

If the Otis King slide rule in [Chris Staecker’s] latest video looks a bit familiar, you might be getting up there in age, or you might remember seeing us talk about one in our collection. Actually, we have two floating around one of the Hackaday bunkers, and they are quite the conversation piece. You can watch the video below.

The device is often mistaken for a spyglass, but it is really a huge slide rule with the scale wrapped around in a rod-shaped form factor. The video says the scale is the same as a 30-inch scale, but we think it is closer to 66 inches.

Continue reading “Unwinding An Unusual Slide Rule” →

Mechanical Calculator Finds Derivatives

January 6, 2025 by 14 Comments

We like mechanical calculators like slide rules, but we have to admit that we had not heard of the Ott Derivimeter that [Chris Staecker] shows us in a recent video. As the name implies, the derivimeter finds the derivative of a function. To do that, you have to plot the function on a piece of paper that the meter can measure.

If you forgot calculus or skipped it altogether, the derivative is the rate of change. If you plot, say, your car’s speed vs time, the parts where you accelerate or decelerate will have a larger derivative (either positive or negative, in the decelerate case). If you hold a steady speed, the derivative will be zero.

Continue reading “Mechanical Calculator Finds Derivatives” →

The Genius Of Slide Rule Precision

May 29, 2024 by 50 Comments

Most people have heard of or seen slide rules, with older generations likely having used these devices in school and at their jobs. As purely analog computers these ingenious devices use precomputed scales on slides, which when positioned to a specific input can give the output to a wide range of calculations, ranging from simple divisions and multiplications to operations that we generally use a scientific calculator for these days. Even so, these simple devices are both very versatile and can be extremely precise, as [Bob, the Science Guy] demonstrates in a recent video.

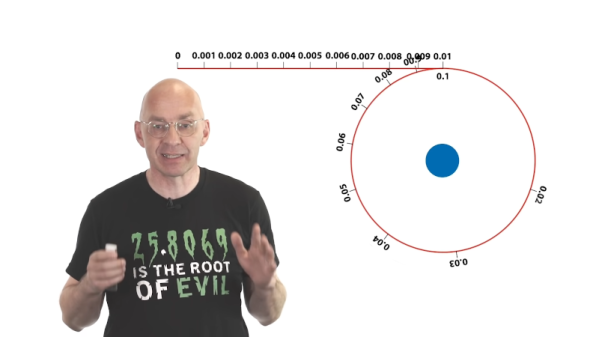
Slide rules at their core are very simple: you got different scales (marked by a label) which can slide relative to each other. Simple slide rules will only have the A through D scales, with an input provided by moving one scale relative to the relevant other scale (e.g. C and D for multiplication/division) after which the result can be read out. Of course, it seems reasonable that the larger your slide rule is, the more precision you can get out of it. Except that if you have e.g. the W1 and W2 scales on a shorter (e.g. 10″) slide rule, you can use those to get the precision of a much larger (20″) slide rule, as [Bob] demonstrates.

Even though slide rules have a steeper learning curve than punching numbers into a scientific calculator, it is hard to argue the benefits of understanding such relationships between the different scales, and why they exist in the first place.

Continue reading “The Genius Of Slide Rule Precision” →