Op-Amp Challenge: Interactive Analog LED Wave Array

May 12, 2023 by Dave Rowntree 20 Comments

A while back, [Chris Lu] was studying how analog circuits, specifically op-amps can be used to perform mathematical operations and wondered if they could be persuaded to solve differential equations, such as the wave equation. After sitting on the idea for a few years, it was time to make it a reality, and the result is an entry into the Op-Amp Challenge.

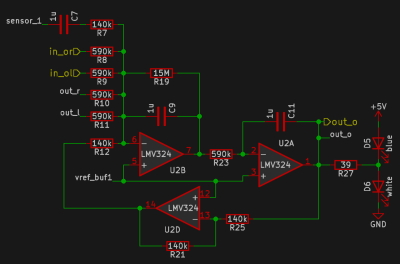Unlike many similar interactive LED matrix displays that are digital in nature (because it’s a lot easier), this design is pure analog, using many, many op-amps. A custom PCB houses a 4×4 array of compute units, each with a blue and white LED indicating the sign and magnitude of the local signal.

The local input signal is provided by an IR photodiode, AC coupled to only respond to change, with every other circuit sharing a sensor to keep it simple. Each circuit is connected to its immediate neighbors on the PCB, and off the PCB via board-to-board connectors. This simple scheme makes this easily scalable if desired in the future.

[Chris] does a great job of breaking down the math involved, which makes this project a neat illustration of how op-amp circuits can implement complex mathematical problems in an easy-to-understand process. Even more op-amps are pressed into service for generating the split-rail voltage reference and for amplifying the weak photodiode signals, but the computation circuit is the star of the show.

We like analog computing a fair bit around these parts. Here’s a little something we were previously drooling over.

Continue reading “Op-Amp Challenge: Interactive Analog LED Wave Array” →

Retrotechtacular: Fire Control Computers In Navy Ships

October 28, 2014 by Kristina Panos 29 Comments

Here is a two-part Navy training film from 1953 that describes the inner workings of mechanical fire control computers. It covers seven mechanisms: shafts, gears, cams, differentials, component solvers, integrators, and multipliers, and does so in the well-executed fashion typical of the era.

Fire control systems depend on many factors that occur simultaneously, not the least of which are own ship’s speed and course, distance to a target, bearing, the target’s speed and course if not stationary, initial shell velocity, and wind speed and direction.

The mechanisms are introduced with a rack and pinion demonstration in two dimensions. Principally speaking, a shaft carries a value based on revolutions. From this, a system can be geared at different ratios.

Cams take this idea further, transferring a regular motion such as rotation to an irregular motion. They do so using a working surface as input and a follower as output. We are shown how cams change rotary motion to linear motion. While the simplest example is limited to a single revolution, additional revolutions can be obtained by extending the working surface. This is usually done with a ball in a groove.

Continue reading “Retrotechtacular: Fire Control Computers In Navy Ships” →