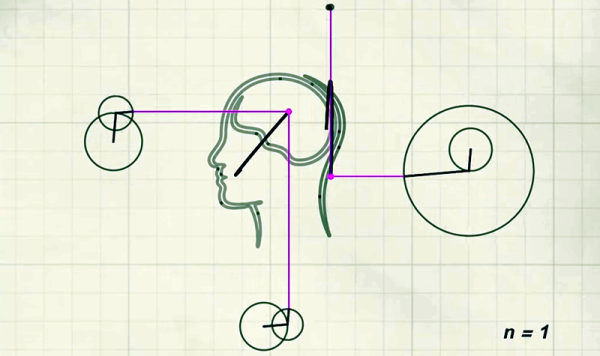
We’ve seen many graphical and animated explainers for the Fourier series. We suppose it is because it is so much fun to create the little moving pictures, and, as a bonus, it really helps explain this important concept. Even if you already understand it, there’s something beautiful and elegant about watching a mathematical formula tracing out waveforms.
[Andrei Ciobanu] has added his own take to the body of animations out there — or, at least, part one of a series — and we were impressed with the scope of it. The post starts with the basics, but doesn’t shy away from more advanced math where needed. Don’t worry, it’s not all dull. There’s mathematical flowers, and even a brief mention of Pink Floyd.
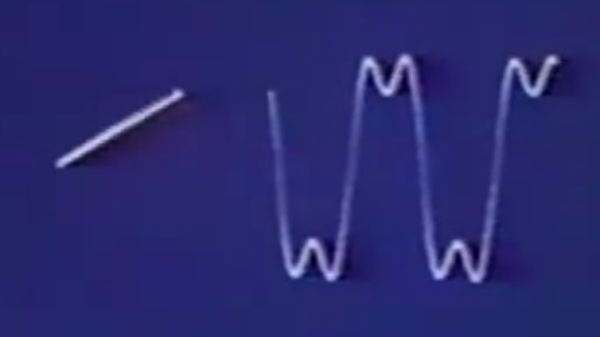
The Fourier series is the basis for much of digital signal processing, allowing you to build a signal from the sum of many sinusoids. You can also go in reverse and break a signal up into its constituent waves.
We were impressed with [Andrei’s] sinusoid Tetris, and it appears here, too. We’ve seen many visualizers for this before, but each one is a little different.