rms

5 Articles

Need A Refresher On RMS?

January 16, 2024 by 21 Comments

If you mostly deal with DC current, you might not think much of root mean square or RMS measurements. Sure, you’ve seen meters that have “true RMS” settings, but what does it mean? If you don’t know — or you want a refresher — watch [Prof MAD’s] recent video explaining the topic.

There are two things to remember when working with RMS. If you put, say, 100VDC through a 100-ohm resistor, you’ll draw 1A and use 100W of power. However, since AC gradually makes its way to a peak value and then starts ramping down immediately, you can’t use the peak value or anything like it to figure out AC power. After all, the voltage is only at that peak for an instant. That’s where RMS comes in. 100 VAC RMS through a 100-ohm resistor will also consume an average of 100W over time.

Continue reading “Need A Refresher On RMS?” →

Hackaday Prize 2023: AC Measurements Made Easy

October 12, 2023 by 17 Comments

When working on simple DC systems, a small low-cost multimeter from the hardware store will get the job done well enough. Often they have the capability for measuring AC, but this is where cheap meters can get tripped up. Unless the waveform is a perfect sinusoid at a specific frequency, their simple algorithms won’t be able to give accurate readings like a high-quality meter will. [hesam.moshiri] took this as a design challenge, though, and built an AC multimeter to take into account some of the edge cases that come up when working with AC circuits, especially when dealing with inductive loads.

The small meter, an upgrade from a previous Arduino version that is now based on the ESP32, is capable of assessing root mean square (RMS) voltage, RMS current, active power, power factor, and energy consumption after first being calibrated using the included push buttons. Readings are given via a small OLED screen and have an accuracy rate of 0.5% or better. The board also includes modern design considerations such as galvanic isolation between the measurement side of the meter and the user interface side, each with its own isolated power supply.  The schematics and bill-of-materials are also available for anyone looking to recreate or build on this design.

With the project built on an easily-accessible platform like the ESP32, it would be possible to use this as a base to measure other types of signals as well. Square and triangle waves, as well as signals with a large amount of harmonics or with varying frequencies, all need different measurement techniques in order to get accurate readings. Take a look at this classic multimeter to see what that entails.

Continue reading “Hackaday Prize 2023: AC Measurements Made Easy” →

Finally, An Open Source Multimeter

June 20, 2019 by 18 Comments

For his Hackaday Prize entry, [Martin] is building an Open Source Multimeter that can measure voltage, current, and power. It’s an amazing build, and you too can build one yourself.

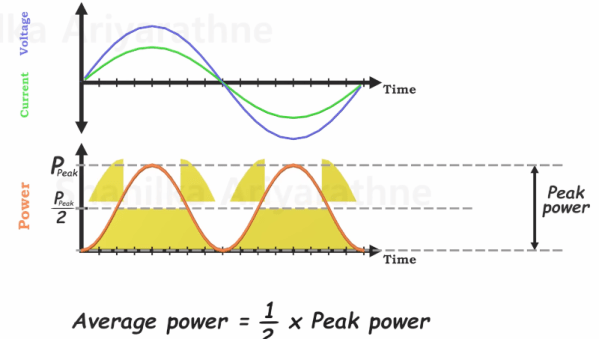
The features for this multimeter consist of voltage mode with a range of +/-6V and +/-60V. There’s a current mode, basically the same as voltage, with a range of +/-60 mA and +/-500mA. Unlike our bright yellow Fluke, there’s also a power mode that measures voltage and current at the same time, with all four combinations of ranges available. There’s a continuity test that sounds a buzzer when the resistance is below 50 Ω, and a component test mode that measures resistors, caps, and diodes. There’s a fully isolated USB interface capable of receiving commands and transmitting data, a real-time clock, and in the future there might be frequency measurement.

This build is based on the STM32F103 microcontroller, uses an old Nokia phone screen, and unlike so many other multimeters, this thing is small. It’s very small. More than small enough to fit in your pocket and forget about it, unlike nearly every other multimeter available. There’s one thing about multimeters, and it’s that the best multimeter is the one that you have in your hands when you need it, and this one certainly fits the bill.

The entire project is being written up on hackaday.io, there’s a GitHub repo for all the hardware and software, and there’s also a video demo covering all the features (available below). This is a stand-out project, and something we desperately want to get our hands on.

The HackadayPrize2019 is Sponsored by:

Continue reading “Finally, An Open Source Multimeter” →

Say It With Me: Root-Mean-Square

April 13, 2017 by 23 Comments

If you measure a DC voltage, and want to get some idea of how “big” it is over time, it’s pretty easy: just take a number of measurements and take the average. If you’re interested in the average power over the same timeframe, it’s likely to be pretty close (though not identical) to the same answer you’d get if you calculated the power using the average voltage instead of calculating instantaneous power and averaging. DC voltages don’t move around that much.

Try the same trick with an AC voltage, and you get zero, or something nearby. Why? With an AC waveform, the positive voltage excursions cancel out the negative ones. You’d get the same result if the flip were switched off. Clearly, a simple average isn’t capturing what we think of as “size” in an AC waveform; we need a new concept of “size”. Enter root-mean-square (RMS) voltage.

To calculate the RMS voltage, you take a number of voltage readings, square them, add them all together, and then divide by the number of entries in the average before taking the square root: \sqrt{\frac{1}{n} \left(v_1^2 + v_2^2 +...+ v_n^2\right)} . The rationale behind this strange averaging procedure is that the resulting number can be used in calculating average power for AC waveforms through simple multiplication as you would for DC voltages. If that answer isn’t entirely satisfying to you, read on. Hopefully we’ll help it make a little more sense.

Continue reading “Say It With Me: Root-Mean-Square” →

Whole House Current Monitoring

July 7, 2010 by 46 Comments

[youtube=http://www.youtube.com/watch?v=HlRBrTTLQFU]

[Debraj Deb] put together a current monitoring device that interfaces with the circuit box at his house. The system is controlled by a PIC 18F4520 and uses an LM358 Op-Amp to rectify the AC signal, as well as an MCP6S21 for range adjustments for detecting both high or low current loads. The data displayed on a character LCD includes average, RMS, and peak current. For now the data is saved to an EEPROM and can be dumped using a serial connection but [Debraj] plans to add a GSM modem so he can send energy use data to his cell phone.

[Thanks Ganesh]