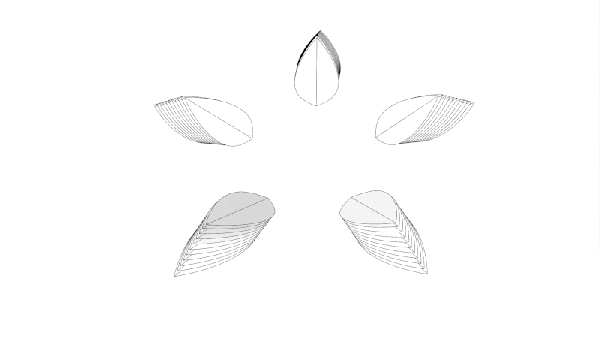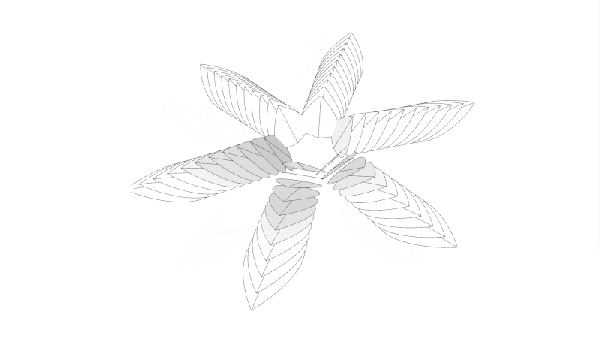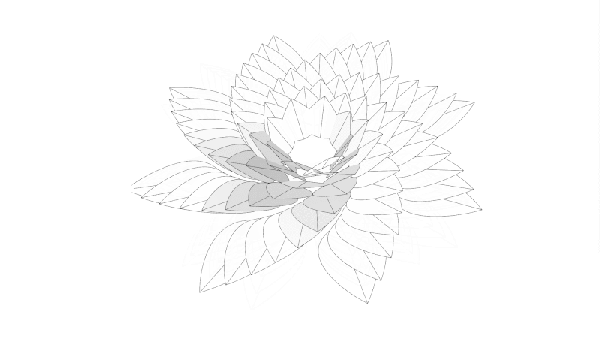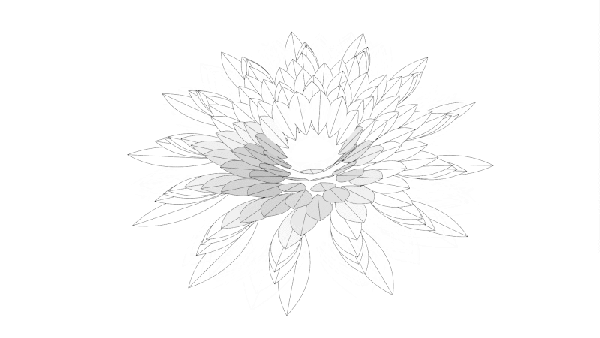
Print Yourself Penrose Wave Tiles As An Excellent Conversation Starter

October 1, 2024 by Lewin Day 11 Comments

Ah, tiles. You can get square ones, and do a grid, or you can get fancier shapes and do something altogether more complex. By and large though, whatever pattern you choose, it will normally end up repeating on some scale or other. That is, unless you go with something like a Penrose Wave Tile. Discovered by mathematician Roger Penrose, they never exactly repeat, no matter how you lay them out.

[carterhoefling14] decided to try and create Penrose tiles at home—with a 3D printer being the perfect route to do it. Creating the tiles was simple—the first step was to find a Penrose pattern image online, which could then be used as the basis to design the 3D part in Fusion 360. From there, the parts were also given an inner wave structure to add further visual interest. The tiles were then printed to create a real-world Penrose tile form.

You could certainly use these Penrose tiles as decor, though we’d make some recommendations if you’re going that path. For one, you’ll want to print them in a way that optimizes for surface quality, as post-processing is time consuming and laborious. If you’re printing in plastic, probably don’t bother using these as floor tiles, as they won’t hold up. Wall tiles, though? Go nuts, just not as a splashback or anything. Keep it decorative only.

You can learn plenty more about Penrose tiling if you please. We do love a bit of maths around these parts, too. If you’ve been making your own topological creation, don’t hesitate to drop us a line.

Tracing In 2D And 3D With Hall Effect Sensors

August 19, 2022 by Lewin Day 11 Comments

Pantographs were once used as simple mechanical devices for a range of tasks, including duplicating simple line drawings. [Tim] decided to make a modern electronic version that spits out G-Code instead.

The design relies on a 3D-printed pantograph assembly, mounted upon a board as a base. A pair of Hall effect sensors are mounted in the pantograph, which, along with a series of neodymium magnets, can be used to measure the angles of the pantograph’s joints. The Hall sensors are read by an Arduino Nano, which computes the angles into movement of the pantograph head and records it as G-Code. This can simply be displayed on the attached LCD display, or offloaded to a computer for storage.

[Tim] explains the basic theory behind the work in an earlier piece, where he built a set of electronic dividers using the same techniques. He didn’t stop there, either. He also built a more complex version that works in 3D that he calls it the Electronic Point Mapper, which can be used to generate point clouds with a 3D-capable pantograph mechanism.

It’s a neat way to learn about geometry, and could even be useful if you’re doing some work in tracing 2D drawings or measuring 3D objects.

Continue reading “Tracing In 2D And 3D With Hall Effect Sensors” →

New Video Series: Designing With Complex Geometry

July 22, 2021 by Tom Nardi 17 Comments

Whether it’s a 3D printed robot chassis or a stained glass window, looking at a completed object and trying to understand how it was designed and put together can be intimidating. But upon closer examination, you can often identify the repeating shapes and substructures that were combined to create the final piece. Soon you might find that the design that seemed incredibly intricate when taken as a whole is actually an amalgamation of simple geometric elements.

This skill, the ability to see an object for its principle components, is just as important for designing new objects as it is for understanding existing ones. As James McBennett explains in his HackadayU course Designing with Complex Geometry, if you want to master computer-aided design (CAD) and start creating your own intricate designs, you’d do well to start with a toolbox of relatively straightforward geometric primitives that you can quickly modify and reuse. With time, your bag of tricks will be overflowing with parametric structures that can be reshaped on the fly to fit into whatever you’re currently working on.

His tool of choice is Grasshopper, a visual programming language that’s part of Rhino. Designs are created using an interface reminiscent of Node-RED or even GNU Radio, with each interconnected block representing a primitive shape or function that can be configured through static variables, interactive sliders, conditional operations, and even mathematical expressions. By linking these modules together complex structures can be generated and manipulated programmatically, greatly reducing the time and effort required compared to a manual approach.

As with many powerful tools, there’s certainly a learning curve for Grasshopper. But over the course of this five part series, James does a great job of breaking things down into easily digestible pieces that build onto each other. By the final class you’ll be dealing with physics and pushing your designs into the third dimension, producing elaborate designs with almost biological qualities.

Of course, Rhino isn’t for everyone. The $995 program is closed source and officially only runs on Windows and Mac OS. But the modular design concepts that James introduces, as well as the technique of looking at large complex objects as a collection of substructures, can be applied to other parametric CAD packages such as FreeCAD and OpenSCAD.

Designing with Complex Geometry is just one of the incredible courses offered through HackadayU, our pay-as-you-wish grad school for hardware hackers. From drones to quantum computing, the current list of courses has something for everyone.

Continue reading “New Video Series: Designing With Complex Geometry” →

Tracking Drone Flight Path Via Video, Using Cameras We Can Get

November 13, 2020 by Roger Cheng 4 Comments

Calculating three-dimensional position from two-dimensional projections are literal textbook examples in geometry, but those examples are the “assume a spherical cow” type of simplifications. Applicable only in an ideal world where the projections are made with mathematically perfect cameras at precisely known locations with infinite resolution. Making things work in the real world is a lot harder. But not only have [Jingtong Li, Jesse Murray et al.] worked through the math of tracking a drone’s 3D flight from 2D video, they’ve released their MultiViewUnsynch software on GitHub so we can all play with it.

Instead of laboratory grade optical instruments, the cameras used in these experiments are available at our local consumer electronics store. A table in their paper Reconstruction of 3D Flight Trajectories from Ad-Hoc Camera Networks (arXiv:2003.04784) listed several Huawei cell phone cameras, a few Sony digital cameras, and a GoPro 3. Video cameras don’t need to be placed in any particular arrangement, because positions are calculated from their video footage. Correlating overlapping footage from dissimilar cameras is a challenge all in itself, since these cameras record at varying framerates ranging from 25 to 59.94 frames per second. Furthermore, these cameras all have rolling shutters, which adds an extra variable as scanlines in a frame are taken at slightly different times. This is not an easy problem.

There is a lot of interest in tracking drone flights, especially those flying where they are not welcome. And not everyone have the budget for high-end equipment or the permission to emit electromagnetic signals. MultiViewUnsynch is not quite there yet, as it tracks a single target and video files were processed afterwards. The eventual goal is to evolve this capability to track multiple targets on live video, and hopefully help reduce frustrating public embarrassments.

[IROS 2020 Presentation video (duration 14:45) requires free registration, available until at least Nov. 25th 2020.]

Tessellations And Modular Origami From Fabric And Paper

January 20, 2020 by Sharon Lin 5 Comments

You may be familiar with origami, the Japanese art of paper folding, but chances are you haven’t come across smocking. This technique refers to the way fabric can be bunched by stitches, often made in a grid-like pattern to create more organized designs. Often, smocking is done with soft fabrics, and you may have even noticed it done on silk blouses and cotton shirts. There are plenty of examples of 18th and 19th century paintings depicting smocking in fashion.

[Madonna Yoder], an origami enthusiast, has documented her explorations in origami tessellations and smocking, including geometric shapes folded from a single sheet of paper and fabric smocked weave patterns. Apart from flat patterns, she has also made chain-linked smocked scarves stitched into a circular pattern and several examples of origami tessellations transferred to fabric smocking. Similar to folds in origami, the stitches used aren’t complex. Rather, the crease pattern defines the final shape once the stitches and fabric are properly gathered together.

Continue reading “Tessellations And Modular Origami From Fabric And Paper” →

This Artist Drags His Feet Across Sand And Snow

January 11, 2020 by Sharon Lin 10 Comments

You may have seen Simon Beck’s work a few years back. The snow artist, known for creating large-scale works of art with nothing but snowshoes, has been creating geometrically inspired fractals and mathematical forms for years. An orienteer and map-maker by day, he typically plans out his works in advance and chooses sites based on their flat terrain. The lack of slopes prevents skiers from traversing the area beforehand and helps with measuring the lines needed to create the drawing.

He starts off by measuring the distance he has to be from the center by using a compass and walking in a straight line towards a point in the distance, making curves based on relative position to other lines. Once the primary lines are made, he measures points along the way using pace counting and joins secondary lines by connecting the points. The lines are generally walked three times to solidify them before filling in the shaded areas. The results are mesmerizing.

He has since expanded to sand art, using the same techniques that gained him fame in ski resorts and national parks on the sandy shores. Unfortunately, tidal patterns, seaweed, and beach debris make it slightly harder to achieve pristine conditions, but he has managed to create some impressive works of art nonetheless.

Continue reading “This Artist Drags His Feet Across Sand And Snow” →

Building Your Own Tensegrity Structure

November 29, 2019 by Sharon Lin 37 Comments

It seems that tensegrity structures are trending online, possibly due to the seemingly impossible nature of their construction. The strings appear to levitate without any sound reason, but if you bend them just the right way they’ll succumb to gravity.

The clue is in the name. Tensegrity is a pormanteau of “tension” and “integrity”. It’s easiest to understand if you have a model in your hand — cut the strings and the structure falls apart. We’re used to thinking of integrity in terms of compression. Most man-made structures rely on this concept of engineering, from the Empire State Building to the foundation of apartment building.

Tensegrity allows strain to be distributed across a structure. While buildings built from continuous compression may not show this property, more elastic structures like our bodies do. These structures can be built on top of smaller units that continuously distribute strain. Additionally, these structures can be contracted and retracted in ways that “compressionegrities” simply can’t exhibit.

How about collapsing the structure? This occurs at the weakest point. Wherever the load has the greatest strain on a structure is where it will likely snap, a property demonstrable in bridges, domes, and even our bodies.

Fascinated? Fortunately, it’s not too difficult to create your own structures.

Continue reading “Building Your Own Tensegrity Structure” →