Tiling a space with a repeated pattern that has no gaps or overlaps (a structure known as a tessellation) is what led mathematician [Gábor Domokos] to ponder a question: how few corners can a shape have and still fully tile a space? In a 2D the answer is two, and a 3D space can be tiled in shapes that have no corners at all, called soft cells.
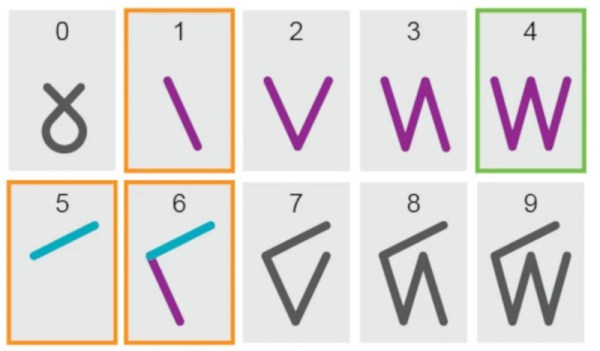
 These shapes can be made in a few different ways, and some are shown here. While they may have sharp edges there are no corners, or points where two or more line segments meet. Shapes capable of tiling a 2D space need a minimum of two corners, but in 3D the rules are different.
These shapes can be made in a few different ways, and some are shown here. While they may have sharp edges there are no corners, or points where two or more line segments meet. Shapes capable of tiling a 2D space need a minimum of two corners, but in 3D the rules are different.
A great example of a natural soft cell is found in the chambers of a nautilus shell, but this turned out to be far from obvious. A cross-section of a nautilus shell shows a cell structure with obvious corners, but it turns out that’s just an artifact of looking at a 2D slice. When viewed in full 3D — which the team could do thanks to a micro CT scan available online — there are no visible corners in the structure. Once they knew what to look for, it was clear that soft cells are present in a variety of natural forms in our world.
[Domokos] not only seeks a better mathematical understanding of these shapes that seem common in our natural world but also wonders how they might relate to aperiodicity, or the ability of a shape to tile a space without making a repeating pattern. Penrose Tiles are probably the most common example.