Month: January 2016

Cyborg Photosynthetic Bacteria!

January 19, 2016 by 4 Comments

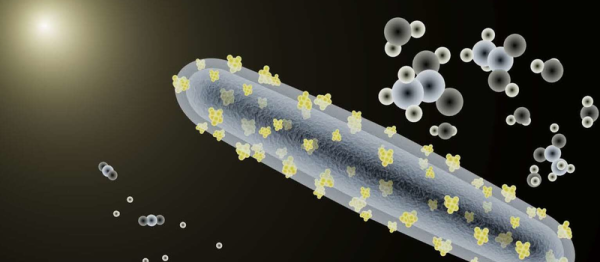
This is weird science. Researchers at Lawrence Berkeley National Laboratory have taken some normal bacteria and made them photosynthetic by adding cadmium sulfide nanoparticles. Cadmium sulfide is what makes the garden-variety photoresistor work. That’s strange enough. But the bacteria did the heavy lifting — they coated themselves in the inorganic cadmium — which means that they can continue to grow and reproduce without much further intervention.

Bacteria are used as workhorses in a lot of chemical reactions these days, and everybody’s trying to teach them new tricks. But fooling them into taking on inorganic light absorbing materials and becoming photosynthetic is pretty cool. As far as we understand, the researchers found a chemical pathway into which the electrons produced by the CdS would fit, and the bacteria took care of the rest. They still make acetic acid, which is their normal behavior, but now they produce much more when exposed to light.

If you want to dig a little deeper, the paper just came out in Science magazine, but it’s behind a paywall. But with a little searching, one can often come up with the full version for free. (PDF).

Or if you’d rather make electricity, instead of acetic acid, from your bacteria be our guest. In place of CdS, however, you’ll need a fish. Biology is weird.

Headline images credit: Peidong Yang

Naviator Drone Uses Its Propellers To Fly And Swim

January 18, 2016 by 40 Comments

Rutgers University just put out a video on a “drone” that can fly and then drop into a body of water, using its propellers to move around. This isn’t the first time we’ve covered a university making sure Skynet can find us even in the bathtub, but this one is a little more manageable for the home experimenter. The robot uses a Y8 motor combination. Each motor pair on its four arms spin in opposite directions, but provide thrust in the same direction. Usually this provides a bit more stability and a lot more redundancy in a drone. In this case we think it helps the robot leave the water and offers a bit more thrust underwater when the props become dramatically less efficient.

We’re excited to see where this direction goes. We can already picture the new and interesting ways one can lose a drone and GoPro forever using this, even with the integral in your toolbox. We’d also like to see if the drone-building community can figure out the new dynamics for this drone and release a library for the less mathematically inclined to play with. Video after the break.

Continue reading “Naviator Drone Uses Its Propellers To Fly And Swim” →

Shmoocon 2016: Hackers For Charity

January 18, 2016 by 4 Comments

To one side of the “Chill Room” at this year’s Shmoocon were a few tables for Hackers for Charity. This is an initiative to make skills-training available for people in Uganda. The organization is completely supported by the hacker community.

Hackers for Charity was founded by Johnny Long about seven years ago. He had been working as a penetration tester but you perhaps know him better from his many books on hacking. Having seen the lack of opportunity in some parts of the world, Johnny started Hackers for Charity as a way to get used electronics and office equipment into the hands of people who needed it most. This led to the foundation of a school in Uganda that teaches technology skills. This can be life-changing for the students who go on to further schooling, or often find clerical or law enforcement positions. Through the charity’s donations the training center is able to make tuition free for about 75% of the student body.

The education is more than just learning to use a word processor. The group has adopted a wide range of equipment and digital resources to make this an education you’d want for your own children. Think Chromebooks, Raspberry Pi, robotics, and fabrication. One really interesting aspect is the use of RACHEL, which is an effort to distribute free off-line educational content. This is a searchable repository of information that doesn’t require an Internet connection. Johnny told me that it doesn’t stop at the schoolroom door; they have the system on WiFi so that anyone in the village can connect and use the resources whether they’re students or not.

Shmoocon does something interesting with their T-shirt sales. They’re not actually selling shirts at all. They’re soliciting $15 donations. You donate, and you get a shirt and a chit — drop you chit in a box to decide where your $15 should go. This year, Hackers for Charity, the EFF, and World Bicycle Relief were the charities to choose from. If you want to help out this 501c3 organization, consider clicking the donate button you’ll find on the sidebar and footer of their webpage.

Mouse Pen From Old Parts

January 18, 2016 by 22 Comments

No offense to [Douglas Engelbart] but the computer mouse has always seemed a bit of a hack to us (and not in the good sense of the word). Sure we’ve all gotten used to them, but unlike a computer keyboard, there is no pre-computer analog to a mouse. There are plenty of alternatives, of course, like touchpads and trackballs, but they never seem to catch on to the extent that the plain old mouse has.

One interesting variation is the pen mouse. These do rely on a pre-computer analog: a pen or pencil. You can buy them already made (and they are surprisingly inexpensive), but what fun is that? [MikB] wanted one and decided to build it instead of buying it.

The main parts of the pen mouse include a cheap mouse with a failing scroll wheel, a bingo pen, and the base from an old web camera. There’s also a normal-sized pen to act as the handpiece. The project is mostly mechanical rather than electrical. [MikB] took the mouse apart and cut the PCB to fit inside the base. The rest of the build is a construction project.

The result appears to work well. [MikB] includes instructions for installing the mouse correctly in Linux. The net effect is like a tablet but doesn’t’ require much space on your desk. We’ve seen plenty of mouse projects in the past, of course. We’ve even seen hacks for a head mouse if that’s your thing.

Up Your Tiny House Game With Stone Age Hacks

January 18, 2016 by 63 Comments

Bare feet, bare hands, and bare chest – if it weren’t for the cargo shorts and the brief sound of a plane overhead, we’d swear the video below was footage that slipped through a time warp. No Arduinos, no CNC or 3D anything, but if you doubt that our Stone Age ancestors were hackers, watch what [PrimitiveTechnology] goes through while building a tile-roofed hut with no modern tools.

The first thing we’ll point out is that [PrimitiveTechnology] is not attempting to be (pre-)historically accurate. He borrows technology from different epochs in human history for his build – tiled roofs didn’t show up until about 5,000 years ago, by which time his stone celt axe would have been obsolete. But the point of the primitive technology hobby is to build something without using any modern technology. If you need a fire, you use a fire bow; if you need an axe, shape a rock. And his 102 day build log details every step of the way. It’s fascinating to watch logs, mud, saplings, rocks and clay come together into a surprisingly cozy structure. Especially awesome if a bit anachronistic is the underfloor central heating system, which could turn the hut into a lovely sauna.

Primitive technology looks like a fascinating hobby with a lot to teach us about how we got to now. But if you’re not into grubbing in the mud, you could always 3D print a clay hut. We’re not sure building an enormous delta-bot is any easier, though.
Continue reading “Up Your Tiny House Game With Stone Age Hacks” →

Running Calculus On An Arduino

January 18, 2016 by 39 Comments

It was Stardate 2267. A mysterious life form known as Redjac possessed the computer system of the USS Enterprise. Being well versed in both computer operations and mathematics, [Spock] instructed the computer to compute pi to the last digit. “…the value of pi is a transcendental figure without resolution” he would say. The task of computing pi presents to the computer an infinite process. The computer would have to work on the task forever, eventually forcing the Redjac out.

Calculus relies on infinite processes. And the Arduino is a (single thread) computer. So the idea of zeno_03running a calculus function on an Arduino presents a seemingly impossible scenario. In this article, we’re going to explore the idea of using derivative like techniques with a microcontroller. Let us be reminded that the derivative provides an instantaneous rate of change. Getting an instantaneous rate of change when the function is known is easy. However, when you’re working with a microcontroller and varying analog data without a known function, it’s not so easy. Our goal will be to get an average rate of change of the data. And since a microcontroller is many orders of magnitude faster than the rate of change of the incoming data, we can calculate the average rate of change over very small time intervals. Our work will be based on the fact that the average rate of change and instantaneous rate of change are the same over short time intervals.

Continue reading “Running Calculus On An Arduino” →

Continuing Education Via Wheel Balancing

January 18, 2016 by 20 Comments

There’s an old saying that you should make things twice. Once to figure out how to build the thing, and again to build it the right way. [Pmbrunelle] must agree. His senior project in college was a machine to balance wheels. It was good enough for him to graduate, but he wanted it to be even better.

The original machine required observation of measurements on an oscilloscope and manual calculations. [Pmbrunelle] added an AVR micro, a better motor drive, and made a host of other improvements. As you can see in the video below, the machine works, but [Pmbrunelle] still wasn’t happy.

Continue reading “Continuing Education Via Wheel Balancing” →