Day: February 22, 2024

The Latest Advancements In Portable N64 Modding

February 22, 2024 by 6 Comments

[Chris Downing] has been in the mod scene a long time, and his 5th GeN64 Portable is his most modern portable Nintendo 64 yet. The new build has an improved form factor, makes smart use of 3D printing and CNC cutting, efficiently uses PCBs to reduce wiring, and incorporates a battery level indicator. That last feature is a real quality of life improvement, nicely complementing the ability to charge over USB-C.

What’s interesting about builds like this is that it’s all about the execution. The basic parts required to mod a classic games console into a portable unit are pretty well understood, and off-the-shelf modules like button assemblies exist to make the job far easier than it was back in the day when all had to be done from scratch. We’ve admired [Chris Downing]’s previous builds, and what differentiates one mod from another really comes down to layout and execution, and that’s where the 5th GeN64 Portable shines. Continue reading “The Latest Advancements In Portable N64 Modding” →

The ELIZA Archaeology Project: Uncovering The Original ELIZA

February 22, 2024 by 30 Comments

Since ELIZA was created by [Joseph Weizenbaum] in the 1960s, its success had led to many variations and ports being written over the intervening decades. The goal of the ELIZA Archaeology Project by Stanford, USC, Oxford and other university teams is to explore and uncover as much of this history as possible, starting with the original 1960s code. As noted in a recent blog post by [Anthony Hay], most of the intervening ‘ELIZA’ versions seem to have been more inspired by the original rather than accurate replicas or extensions of the original. This raises the question of what the original program really looked like, a question which wasn’t answered until 2020 when the original source code was rediscovered. Continue reading “The ELIZA Archaeology Project: Uncovering The Original ELIZA” →

A man standing next to a log holds a wooden mallet and a grey froe with a wooden handle. The froe's long straight blade sits atop the end of the log. Several cuts radiate out from the center of the log going through the length of the wood.

Making Wooden Shingles With Hand Tools

February 22, 2024 by 23 Comments

While they have mostly been replaced with other roofing technologies, wooden shingles have a certain rustic charm. If you’re curious about how to make them by hand, [Harry Rogers] takes us through his friend [John] making some.

There are two primary means of splitting a log for making shingles (or shakes). The first is radial, like one would cut a pie, and the other is lateral, with all the cuts in the same orientation. Using a froe, the log is split in progressively smaller halves to control the way the grain splits down the length of the log and minimize waste. Larger logs result in less waste and lend themselves to the radial method, while smaller logs must be cut laterally. Laterally cut shingles have a higher propensity for warping and other issues, but will work when larger logs are not available.

Once the pieces are split out of the log, they are trimmed with an axe, including removing the outer sapwood which is the main attractant for bugs and other creatures that might try eating your roof. Once down to approximately the right dimensions, the shingle is then smoothed out on a shave horse with a draw knife. Interestingly, the hand-made shingles have a longer lifespan than those sawn since the process works more with the grain of the wood and introduces fewer opportunities for water to seep into the shingles.

If you’re looking for something more solarpunk and less cottagecore for your house, maybe try a green solar roof, and if you’ve got a glass roof, try cleaning it with the Grawler.

Continue reading “Making Wooden Shingles With Hand Tools” →

Solar E-Ink Weather Station Works On Dark Days, Too

February 22, 2024 by 11 Comments

One way to get through the winter doldrums is to take notice of the minuscule positive changes in weather as spring approaches. Although much of the US is experiencing a particularly warm month, that’s not the case in Germany where [rsappiawf] resides. Even so, they are having a good time charting the weather on their new solar-powered E-ink weather station.

And in spite of the dark winter days, the device has been delivering weather updates for over a week on solar power alone. The brains of this operation is an ESP32 S3 Mini, which [rsappiawf] operated on a little bit. For starters, they removed the integrated RGB LED in order to save precious milliamps. Then they upgraded the voltage regulator to a TPS73733DCQR.

[rsappiawf] also has a TPL5110 power timer breakout module in the mix, which saves even more power by only turning on every once in a while according to the potentiometer setting, and only then turning on the project’s power. Check out the brief demo after the break, including the cool sliding action into the 3D-printed holder.

There’s a lot you can do to lower power consumption in a project like this. Here’s one that will go 60 days on a charge.

Continue reading “Solar E-Ink Weather Station Works On Dark Days, Too” →

The Book8088 Gets A Post-Hype Review

February 22, 2024 by 24 Comments

Last year, a couple of rather unusual computers emerged from China: a 386sx-based palmtop and an 8088-based mini-laptop. The average person isn’t exactly clamoring for a DOS machine these days, but they attracted quite a bit of interest among the retrocomputing scene. Now the dust has settled, [The Retro Shack] has taken a Book 8088 and given it an honest review. Do you need portable 1980s computing in your life, and if so it this the machine to give you it?

The first impression of the machine is just how svelte it is, being like a small but chunky netbook. He explores the hardware and finds as expected an NEC V20 instead of the Intel part running the show, and what would have been a hugely expanded DOS PC back in the day with its VGA and sound card, not to mention a solid state hard drive.

We’re overcome with a bit of nostalgia here at the sight of DOS running Lemmings, and on a machine we’d have given anything to own back in the 1980s. His final conclusion is that it’s a very nice little PC but around $160 seems a little much for what is essentially a toy. We have sadly to agree with him though we really want one, though noting that such a machine would have retailed for a huge amount more than that in 1980s dollars and we’d have considered it a huge bargain then.

If you’re still curious, we covered the arrival of these machines last year.

Continue reading “The Book8088 Gets A Post-Hype Review” →

2024 Hackaday Europe Call For Participation Extended

February 22, 2024 by 4 Comments

Good news, procrastineers! A few folks asked us for a little more time to get their proposals together for our upcoming 2024 Hackaday Europe event in Berlin, and we’re listening. So now you’ve got an extra week – get your proposals for talks or workshops in before February 29th.

[Joey Castillo]’s awesome custom touchpad
Hackaday Europe is a two-day event taking place April 13th and 14th in Berlin, Germany. Saturday the 13th is the big day, with a full day of badge hacking, talks, music, and everything else. We’ve got the place booked until 2 AM, so get your sleep the night before. Sunday is a half-day of brunch, lightning talks, and showing off the badge hacks from the day before. And if you’re in town on Friday the 12th, we’ll be going out in the evening for drinks and dinner, location TBA but hopefully closer than where we ended up last year!

The badge is going to be a re-spin of the Supercon badge for all of you who couldn’t fly out to the US last November. There are no secrets anymore, so get your pre-hacks started now. We’ve seen some sweet all-analog hacks, some complete revisions of the entire firmware loadout, and, of course, all sorts of awesome hardware bodged onto it. Heck, we even saw Asteroids and DOOM. But we haven’t seen any native Jerobeam Fenderson-style oscilloscope music. You’ve got your homework.

What to Bring?

A few other people have asked if they could bring in (art) projects to show and share. Of course! Depending on the scale, though, you may need to contact us beforehand. If it’s larger than a tower PC, get in touch with us, and we’ll work it out. Smaller hacks, projects in progress, and anything you want to bring along to show and inspire others with, are, of course, welcome without any strings attached.

What else might you need? A computer of your choice and a micro USB cable for programming the badge. There will be soldering stations, random parts, and someone will probably be able to lend you nearly any other piece of gear, so you can pack light if you want to. But you don’t have to.

If you’d like to attend but you don’t have tickets yet – get them soon! Space is limited, and we tend to sell out. Or better yet, submit a talk and sneak in the side door. We’d love to hear what you’ve got going on, and we can’t wait to see you all.

Filters Are In Bloom

February 22, 2024 by 3 Comments

If you are a fan of set theory, you might agree there are two sets of people who write computer programs: those who know what a Bloom filter is and those who don’t. How could you efficiently test to see if someone is one set or another? Well, you could use a Bloom filter.  [SamWho] takes us through the whole thing in general terms that you could apply in any situation.

The Bloom filter does perform a trade-off for its speed. It is subject to false positives but not false negatives. That is, if a Bloom filter algorithm tells you that X is not part of a set, it is correct. But if it tells you it is, you may have to investigate more to see if that’s true.

If it can’t tell you that something is definitely in a set, why bother? Usually, when you use a Bloom filter, you want to reduce searching through a huge amount of data. The example in the post talks about having a 20-megabyte database of “bad” URLs. You want to warn users if they enter one, but downloading that database is prohibitive. But a Bloom filter could be as small as 1.8 megabytes. However, there would be a 1 in 1000 chance of a false positive.

Increase the database size to 3.59 megabytes, and you can reduce false positives to one in a million. Presumably, if you got a positive, you could accept the risk it is false, or you could do more work to search further.

Imagine, for example, a web cache device or program. Many web pages are loaded one time and never again. If you cache all of them, you’ll waste a lot of time and push other things out of the cache. But if you test a page URL with a Bloom filter, you can improve things quite a bit. If the URL may exist in the Bloom filter, then you’ve probably seen it before, so you might want to cache it.

If it says you haven’t, you can add it to the filter so if it is ever accessed again, it will cache. Sure, sometimes a page will show a false positive. So what? You’ll just cache the page on the first time, which is what you did before, anyway. If that happens only 0.1% of the time, you still win.

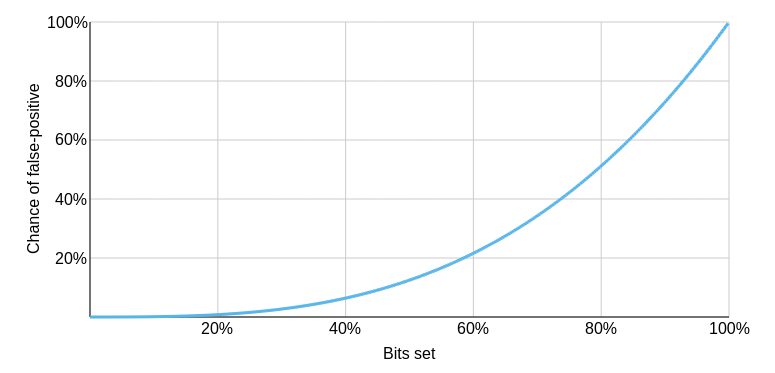
In simple terms, the Bloom filter hashes each item using three different algorithms and sets bits in an array based on the result. To test an item, you compute the same hashes and see if any of the corresponding bits are set to zero. If so, the item can’t be in the set. Of course, there’s no assurance that all three bits being set means the set contains the item. Those three bits might be set for totally different items.

Why does increasing the number of bits help? The post answers that and looks at other optimizations like a different number of hash functions and counting.

The post does a great job of explaining the filter but if you want a more concrete example in C, you might want to read this post next. Or search for code in your favorite language. We’ve talked about Python string handling with Bloom filters before. We’ve even seen a proposal to add them to the transit bus.