fourier transform

20 Articles

Taking Polyphony To A New Level

May 6, 2026 by 4 Comments

There are all manner of musical synthesis techniques, from the early electromechanical instruments through analogue tape systhesis, the all-electronic waveform synthesisers of the 1960s onwards, and Yamaha’s FM systhesis of the 1980s, to name but a few. One of the attributes of such a machine lies in how many voices it has, or in simple terms, how many notes it can play simultaneously. Electronic complexity limited those early synths, but what happens on an FPGA where vast numbers of circuits can be made with little extra cost? [Tsuneo.Ohnaka] is pushing the envelope a little, by cramming 10240 individually controllable oscillators onto a Terasic DE10-nano FPGA board.

While this thing can in theory generate 10240 different notes at once, in practice that doesn’t mean it has 10240 voices. Instead he calls it a spectrum engine, in that with such a large number of oscillators all with individually controllable frequency, phase, and amplitude, he’s made the part of all those Fourier transform maths where all the different frequencies are combined, in hardware. It’s as though you had a sound card which wasn’t based around a DAC fed with samples, instead all those spectrum points you’d derive from a Fourier transform. Because it’s a massive parallel array of real oscillators it all happens concurrently, instantaneously in real time, and is not held back by the processing constraints of a microprocessor. Think of it as something akin to a software defined radio transmitter, but for the world of audio synthesis.

In that light, it can emulate all those other forms of audio synthesis driven by software, but without the software overhead of generating the waveforms. It’s certainly a different approach to generating audio from a computer, and he’s posted a cacophonic demo video below of it as an 80-voice polyphonic synthesiser. We like it.

Continue reading “Taking Polyphony To A New Level” →

Two very similar diffraction patterns are shown, in patterns of green dots against a blue background. The left image is labelled "Kompressions-algorithmus", and the one on the right is labelled "Licht & Zweibelzellen".

Why Diffraction Gratings Create Fourier Transforms

January 27, 2026 by 9 Comments

When last we saw [xoreaxeax], he had built a lens-less optical microscope that deduced the structure of a sample by recording the diffraction patterns formed by shining a laser beam through it. At the time, he noted that the diffraction pattern was a frequency decomposition of the specimen’s features – in other terms, a Fourier transform. Now, he’s back with an explanation of why this is, deriving equations for the Fourier transform from the first principles of diffraction (German video, but with auto-translated English subtitles. Beware: what should be “Huygens principle” is variously translated as “squirrel principle,” “principle of hearing,” and “principle of the horn”).

The first assumption was that light is a wave that can be adequately represented by a sinusoidal function. For the sake of simplicity (you’ll have to take our word for this), the formula for a sine wave was converted to a complex number in exponential form. According to the Huygens principle, when light emerges from a point in the sample, it spreads out in spherical waves, and the wave at a given point can therefore be calculated simply as a function of distance. The principle of superposition means that whenever two waves pass through the same point, the amplitude at that point is the sum of the two. Extending this summation to all the various light sources emerging from the sample resulted in an infinite integral, which simplified to a particular form of the Fourier transform.

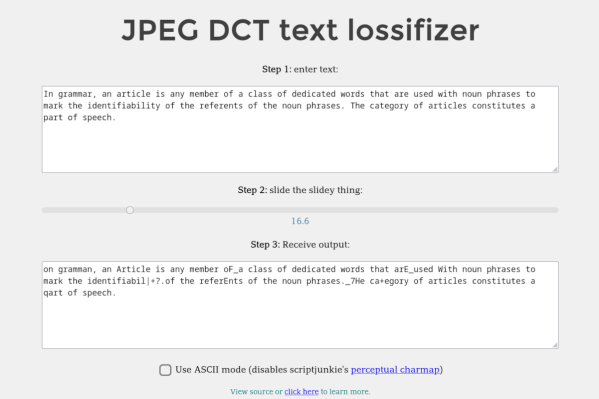
One surprising consequence of the relation is the JPEG representation of a micrograph of some onion cells. JPEG compression calculates the Fourier transform of an image and stores it as a series of sine-wave striped patterns. If one arranges tiles of these striped patterns according to stripe frequency and orientation, then shades each tile according to that pattern’s contribution to the final image, one gets a speckle pattern with a bright point in the center. This closely resembles the diffraction pattern created by shining a laser through those onion cells.

For the original experiment that generated these patterns, check out [xoreaxeax]’s original ptychographical microscope. Going in the opposite direction, researchers have also used physical structures to calculate Fourier transforms.

Continue reading “Why Diffraction Gratings Create Fourier Transforms” →

The Fourier transform

The Unreasonable Effectiveness Of The Fourier Transform

January 7, 2026 by 32 Comments

A talk, The Unreasonable Effectiveness of the Fourier Transform, was presented by [Joshua Wise] at Teardown 2025 in June last year. Click-through for the notes or check out the video below the break for the one hour talk itself.

The talk is about Orthogonal Frequency Division Multiplexing (OFDM) which is the backbone for radio telecommunications these days. [Joshua] tries to take an intuitive view (rather than a mathematical view) of working in the frequency domain, and trying to figure out how to “get” what OFDM is (and why it’s so important). [Joshua] sent his talk in to us in the hope that it would be useful for all skill levels, both folks who are new to radio and signal processing, and folks who are well experienced in working in the frequency domain.

If you think you’ve seen “The Unreasonable Effectiveness of $TOPIC” before, that’s because hacker’s can’t help but riff on the original The Unreasonable Effectiveness of Mathematics in the Natural Sciences, wherein a scientist wonders why it is that mathematical methods work at all. They seem to, but how? Or why? Will they always continue to work? It’s a mystery.

Hidden away in the notes and at the end of his presentation, [Joshua] notes that every year he watches The Fast Fourier Transform (FFT): Most Ingenious Algorithm Ever? and every year he understands a little more.

If you’re interested in OFDM be sure to check out AI Listens To Radio.

Continue reading “The Unreasonable Effectiveness Of The Fourier Transform” →

What Is The Fourier Transform?

September 12, 2025 by 20 Comments

Over at Quanta Magazine [Shalma Wegsman] asks What Is the Fourier Transform?

[Shalma] begins by telling you a little about Joseph Fourier, the French mathematician with an interest in heat propagation who founded the field of harmonic analysis in the early 1800s.

Fourier’s basic insight was that you can represent everything as a sum of very basic oscillations, where the basic oscillations are sine or cosine functions with certain parameters. [Shalma] explains that the biology of our ear can do a similar thing by picking the various notes out from a tune which is heard, but mathematicians and programmers work without the benefit of evolved resonant hairs and bone, they work with math and code.

[Shalma] explains how frequency components can be discovered by trial and error, multiplying candidate frequencies with the original function to see if there are large peaks, indicating the frequency is a component, or if the variations average to zero, indicating the frequency is not a component. [Shalma] tells how even square waves can be modeled with an infinite set of frequencies known as the Fourier series.

Taking a look at higher-dimensional problems [Shalma] mentions how Fourier transforms can be used for graphical compression by dropping the high frequency detail which our eyes can barely perceive anyway. [Shalma] gives us a fascinating look at the 64 graphical building blocks which can be combined to create any possible 8×8 image.

[Shalma] then mentions James Cooley and John Tukey and the development of the Fast Fourier Transform in the 1960s. This mathematical tool has been employed to study the tides, to detect gravitational waves, to develop radar and magnetic resonance imaging, and to support signal processing and data compression. Even quantum mechanics finds use for harmonic analysis, and [Shalma] explains how it relates to the uncertainty principle. The Fourier transform has spread through pure mathematics and into number theory, too.

[Shalma] closes with a quote from Charles Fefferman: “If people didn’t know about the Fourier transform, I don’t know what percent of math would then disappear, but it would be a big percent.”

If you’re interested in the Fourier transform and want to dive deeper we would encourage you to read The Fastest Fourier Transform In The West and Even Faster Fourier Transforms On The Raspbery Pi Zero.

Header image: Joseph Fourier, Attributed to Pierre-Claude Gautherot, Public domain.

Projector on left with red arrow pointing towards object, another red arrow points towards a piece of paper and then camera.

Pictures From Paper Reflections And A Single Pixel

June 29, 2025 by 27 Comments

Taking a picture with a single photoresistor is a brain-breaking idea. But go deeper and imagine taking that same picture with the same photoresistor, but without even facing the object. [Jon Bumstead] did exactly that with compressed sensing and a projector. Incredibly, the resulting image is from the perspective of the projector, not the “camera”.

This camera setup is very similar to one we’ve seen before, but far more capable. The only required electronics are a small projector and a single photodiode. The secret sauce in this particular design lies in the pattern projected and the algorithm to parse the data.

Continue reading “Pictures From Paper Reflections And A Single Pixel” →

Is The Frequency Domain A Real Place?

May 16, 2024 by 60 Comments

When analyzing data, one can use a variety of transformations on the data to massage it into a form that works better to tease out the information one is interested in. One such example is the application of the Fourier transform, which transforms a data set from the time domain into the frequency domain. Yet what is this frequency domain really? After enticing us to follow the white rabbit down a sudden plummet into the intangible question of what is and what is not, [lcamtuf] shows us around aspects of the frequency domain and kin.

One thing about the (discrete) Fourier transform is that it is excellent at analyzing data that consists out of sinewaves, such as audio signals. Yet when using the Fourier transform for square waves, the resulting output is less than useful, almost as if square waves are not real. Similarly, other transforms exist which work great for square waves, but turn everything else into meaningless harmonics. Starting with the discrete cosine transform (DCT), this gets us into Walsh and Hadamard matrices and the Walsh-Hadamard Transform (WHT), and their usage with transforming data from the time into the frequency domain.

Ultimately it would seem that the frequency domain is as real as it needs to be, albeit that its appearance is wholly dependent on the algorithm used to create it, whether this the DFT, DCT, WHT or something else entirely.

Your Text Needs More JPEG

March 19, 2024 by 22 Comments

We’ve all been victims of bad memes on the Internet, but they’re not all just bad jokes gone wrong. Some are simply bad as a result of being copies-of-copies, as each reposter adds another layer of compression to an already lossy image format like JPEG. Compression can certainly be a benefit in areas like images and videos, but [Michal] had a bit of a fever dream imagining this process applied to text. Rather than let the idea escape, he built the Lossifizer to add JPEG-like compression to text.

JPEG compression uses a system similar to the fast Fourier transform (FFT) called the discrete cosine transform (DCT) to reduce the amount of data in an image by essentially removing some frequency information. The data lost is often not noticeable to the human eye, at least until it gets out of hand. [Michal]’s system performs the same transform on text instead, with a slider to control the “amount of JPEG” in the output text. The code for this script uses a “perceptual” character map, clustering similarly-looking and similarly-sounding characters next to each other, resembling “leet speak” from days of yore, although at high enough compression this quickly gets out of hand.

One of the quirks that [Michal] discovered is that certain AI chat bots have a much less difficult time interpreting this JPEG-ified text than a human probably would have, which provides a bit of insight into how some of these algorithms might be functioning under the hood. For some more insight into how JPEG actually works on images, we posted about a deep dive into the image format a while back.