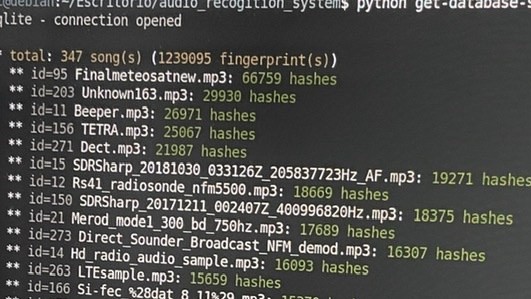
Hash Functions With The Golden Ratio

April 25, 2025 by Bryan Cockfield 9 Comments

In the realm of computer science, it’s hard to go too far without encountering hashing or hash functions. The concept appears throughout security, from encryption to password storage to crypto, and more generally whenever large or complex data must be efficiently mapped to a smaller, fixed-size set. Hashing makes the process of looking for data much faster for a computer than performing a search and can be incredibly powerful when mastered. [Malte] did some investigation into hash functions and seems to have found a method called Fibonacci hashing that not only seems to have been largely forgotten but which speeds up this lookup process even further.

In a typical hashing operation, the data is transformed in some way, with part of this new value used to store it in a specific location. That second step is often done with an integer modulo function. But the problem with any hashing operation is that two different pieces of data end up with the same value after the modulo operation is performed, resulting in these two different pieces of data being placed at the same point. The Fibonacci hash, on the other hand, uses the golden ratio rather than the modulo function to map the final location of the data, resulting in many fewer instances of collisions like these while also being much faster. It also appears to do a better job of using the smaller fixed-size set more evenly as a consequence of being based around Fibonacci numbers, just as long as the input data doesn’t have a large number of Fibonacci numbers themselves.

Going through the math that [Malte] goes over in his paper shows that, at least as far as performing the mapping part of a hash function, the Fibonacci hash performs much better than integer modulo. Some of the comments mention that it’s a specific type of a more general method called multiplicative hashing. For those using hash functions in their code it might be worth taking a look at either way, and [Malte] admits to not knowing everything about this branch of computer science as well but still goes into an incredible amount of depth about this specific method. If you’re more of a newcomer to this topic, take a look at this person who put an enormous bounty on a bitcoin wallet which shows why reverse-hashing is so hard.

Fitting A Spell Checker Into 64 KB

March 26, 2025 by Bryan Cockfield 16 Comments

By some estimates, the English language contains over a million unique words. This is perhaps overly generous, but even conservative estimates generally put the number at over a hundred thousand. Regardless of where the exact number falls between those two extremes, it’s certainly many more words than could fit in the 64 kB of memory allocated to the spell checking program on some of the first Unix machines. This article by [Abhinav Upadhyay] takes a deep dive on how the early Unix engineers accomplished the feat despite the extreme limitations of the computers they were working with.

Perhaps the most obvious way to build a spell checker is by simply looking up each word in a dictionary. With modern hardware this wouldn’t be too hard, but disks in the ’70s were extremely slow and expensive. To move the dictionary into memory it was first whittled down to around 25,000 words by various methods, including using an algorithm to remove all affixes, and then using a Bloom filter to perform the lookups. The team found that this wasn’t a big enough dictionary size, and had to change strategies to expand the number of words the spell checker could check. Hash compression was used at first, followed by hash differences and then a special compression method which achieved an almost theoretically perfect compression.

Although most computers that run spell checkers today have much more memory as well as disks which are orders of magnitude larger and faster, a lot of the innovation made by this early Unix team is still relevant for showing how various compression algorithms can be used on data in general. Large language models, for one example, are proving to be the new frontier for text-based data compression.

Hacking An IoT Camera Reveals Hard-Coded Root Password

July 24, 2024 by Dan Maloney 24 Comments

Hacking — at least the kind where you’re breaking into stuff — is very much a learn-by-doing skill. There’s simply no substitute for getting your hands dirty and just trying something. But that doesn’t mean you can’t learn something by watching, with this root password exploit on a cheap IP video camera being a good look at the basics.

By way of background on this project, [Matt Brown] had previously torn into a VStarcam CB73 security camera, a more or less generic IP camera that he picked up on the cheap, and identified a flash memory chip from which he extracted the firmware. His initial goal was to see if the camera was contacting sketchy servers, and while searching the strings for the expected unsavory items, he found hard-coded IP addresses plus confirmation that the camera was running some Linux variant.

With evidence of sloppy coding practices, [Matt] set off on a search for a hard-coded root password. The second video covers this effort, which started with finding UART pins and getting a console session. Luckily, the bootloader wasn’t locked, which allowed [Matt] to force the camera to boot into a shell session and find the root password hash. With no luck brute-forcing the hash, he turned to Ghidra to understand the structure of a suspicious program in the firmware called encoder. After a little bit of poking and some endian twiddling, he was able to identify the hard-coded root password for every camera made by this outfit, and likely others as well.

Granted, the camera manufacturer made this a lot easier than it should have been, but with a lot of IoT stuff similarly afflicted by security as an afterthought, the skills on display here are probably broadly applicable. Kudos to [Matt] for the effort and the clear, concise presentation that makes us want to dig into the junk bin and get hacking.

Continue reading “Hacking An IoT Camera Reveals Hard-Coded Root Password” →

NTP server heated with Bitcoin mining dongles

Bitcoin Mining ASICs Repurposed To Keep NTP Server On Track

January 12, 2022 by Dan Maloney 27 Comments

They say time is money, but if that’s true, money must also be time. It’s all figurative, of course, but in the case of this NTP server heater powered by Bitcoin mining dongles, money actually does become time.

This is an example of the lengths to which Network Time Protocol aficionados will go in search of slightly better performance from their NTP servers. [Folkert van Heusden], having heard that thermal stability keeps NTP servers happy, used a picnic cooler as an environmental chamber for his Pi- and GPS-based NTP rig. Heat is added to the chamber thanks to seven Block Erupter ASIC miner dongles, which are turned on by a Python script when a microcontroller sends an MQTT message that the temperature has dropped below the setpoint.

Each dongle produces about 2.5 Watts of heat when it’s working, making them pretty effective heaters. Alas, heat is all they produce at the moment — [Folkert] just has them working on the same hash over and over. He does say that he has plans to let the miners do useful work at some point, not so much for profit but to at least help out the network a bit.

This seems like a bit of a long way around to solve this problem, but since the mining dongles are basically obsolete now — we talked about them way back in 2013 — it has a nice hacky feeling to it that we appreciate.

All Your Passwords Are Belong To FPGA

May 15, 2020 by Tom Nardi 26 Comments

When used for cracking passwords, a modern high-end graphics card will absolutely chew through “classic” hashing algorithms like SHA-1 and SHA-2. When a single desktop machine can run through 50+ billion password combinations per second, even decent passwords can be guessed in a worryingly short amount of time. Luckily, advanced password hashing functions such as bcrypt are designed specifically to make these sort of brute-force attacks impractically slow.

Cracking bcrypt on desktop hardware might be out of the question, but the folks over at [Scattered Secrets] had a hunch that an array of FPGAs might be up to the task. While the clock speed on these programmable chips might seem low compared to a modern CPUs and GPUs, they don’t have all that burdensome overhead to contend with. This makes the dedicated circuitry in the FPGA many times more efficient at performing the same task. Using a decade-old FPGA board intended for mining cryptocurrency, the team was able to demonstrate a four-fold performance improvement over the latest generation of GPUs.

After seeing what a single quad FPGA board was capable of, the [Scattered Secrets] team started scaling the concept up. The first version of the hardware crammed a dozen of the ZTEX FPGA boards and a master control computer computer into a standard 4U server case. For the second version, they bumped that up to 18 boards for a total of 72 FPGAs, and made incremental improvements to the power and connectivity systems.

Each 4U FPGA cracker is capable of 2.1 million bcrypt hashes per second, while consuming just 585 watts. To put that into perspective, [Scattered Secrets] says you’d need at least 75 Nvidia RTX-2080Ti graphics cards to match that performance. Such an array would not only take up a whole server rack, but would burn through a staggering 25 kilowatts. Now might be a good time to change your password to something longer, or finally get onboard with 2FA.

We’ve covered attempts to reverse engineer hardware designed for cryptocurrency mining, but those were based around application-specific integrated circuits (ASICs) which by definition are very difficult to repurpose. On the other hand, disused FPGA-based miners offer tantalizing possibilities; once you wrap your mind around how they work, anyway.

[Thanks to Piejoe for the tip.]

Name That Unknown RF Signal With A Little FFT Magic

February 11, 2020 by Dan Maloney 27 Comments

Time was once that the amateur radio bands were an aurally predictable place. Spinning the dial up and down the bands, one heard familiar sounds – the staccato of Morse, the [Donald Duck] of sideband voice transmissions, and the occasional flute-like warble of radioteletype signals. Now, the ham bands are full of exotic signals encoding all manner of digital signals, each one with a unique sound and unique demodulation needs. What’s a ham to do?

Help is on the way. [José Carlos Rueda] has made progress toward automatically classifying unknown signals by modifying a Shazam-like app. Shazam is a popular smartphone app that listens to a few seconds of a song, creates an audio fingerprint of it, and searches a massive database of songs for a match. [Rueda] used a homebrew version of the app to search a SQL-lite database of audio fingerprints populated not with a playlist of popular music, but with samples from every known signal type in the Signal Identification Wiki. The database contains hashes for an FFT of each sample, which can be easily searched. With a five to ten second sample of a signal, captured either live over a microphone or from a recording, he is able to identify the signal automatically.

Whether it be the weird, dissonant wail of PSK-31 or the angry buzzing of PACTOR, the goings-on across the bands no longer have to remain a mystery. We really like the idea here, and wonder if it can be expanded upon to visually decode signals based on their waterfall signatures using TensorFlow. There are some waterfall examples in [Danie Conradie]’s excellent article on RF modulation that could get you started.

[via RTL-SDR.com]

Using Lookup Tables To Make The Impossible Possible

January 10, 2020 by Dan Maloney 60 Comments

Embarrassing confession time: I never learned my multiplication tables in grade school. Sure, I had the easy tables like the twos and the fives down, but if asked what 4 x 7 or 8 x 6 was, I’d draw a blank. As you can imagine, that made me a less than stellar math student, and I was especially handicapped on time-limited tests with lots of long multiplication problems. The standard algorithm is much faster when you’ve committed those tables to memory, as I discovered to my great woe.

I was reminded of this painful memory as I watched Charles Lohr’s 2019 Supercon talk on the usefulness and flexibility of lookup tables, or LUTs, and their ability to ease or even completely avoid computationally intensive operations. Of course most LUT implementations address problems somewhat more complex than multiplication tables, but they don’t have to. As Charles points out, even the tables of sines and logarithms that used to populate page after page in reference books have been ported to silicon, where looking up the correct answer based on user input is far easier than deriving the answer computationally.

Yes, this is a Minecraft server all thanks to LUTs.

One of the most interesting examples of how LUTs can achieve the seemingly impossible lies in an old project where Charles attempted to build a Minecraft server on an ATMega168. Sending chunks (the data representations of a portion of the game world) to clients is the essential job of a Minecraft server, and on normal machines that involves using data compression. Rather than trying to implement zlib on an 8-bit microcontroller, he turned to a LUT that just feeds the raw bytes to the client, without the server having the slightest idea what any of it means. A similar technique is used by some power inverters, which synthesize sine wave output by feeding one full cycle of values to a DAC from a byte array. It’s brute force, but it works.

Another fascinating and unexpected realization is that LUTs don’t necessarily have to be software. Some can be implemented in completely mechanical systems. Charles used the example of cams on a shaft; in a car’s engine, these represent the code needed to open and close valves at the right time for each cylinder. More complicated examples are the cams and gears once found in fire control computers for naval guns, or the programming cards used for Jacquard looms. He even tips his hat to the Wintergatan marble machine, with its large programming drum and pegs acting as a hardware LUT.

I found Charles’ talk wide-ranging and fascinating. Originally I thought it would be an FPGA-heavy talk, but he didn’t actually get to the FPGA-specific stuff until the very end. That worked out fine, though — just hearing about all the cool problems a LUT can solve was worth the price of admission.

And for the curious, yes, I did eventually end up memorizing the multiplication tables. Oddly, it only clicked for me after I started playing with numbers and seeing their relationships using my first calculator, which ironically enough probably used LUTs to calculate results.

Continue reading “Using Lookup Tables To Make The Impossible Possible” →