There are a lot of ways to tell time, but pretty much all of them involve some sort of sequential scale — the hands sweeping across the face of an analog clock comes to mind, as does the incremental changes of a digital clock. Clocks are predictable by their very nature, and therefore somewhat boring.
This nonsequential gear clock aims to break that predictability and make for a timepiece that’s just a little bit different. It’s the work of [Tony Goacher], who clearly put a lot of work into it and pulled out nearly every tool in the shop while doing it. He started with a laser-cut plywood prototype to get the basics worked out — a pair of nested rings with internal gear teeth, each hanging on a stepper-driven pinion. The inner ring represents hours and the outer minutes, with the numbers on each randomly distributed — more or less, since no two sequential numbers are positioned more than five seconds of rotation apart.
The finished version of the clock is rendered in brass, acrylic, hardwood, and a smattering of aluminum, with a case reminiscent of the cathedral radios of yore. There are some really nice touches, like custom-made brass screws, a CNC-engraved brass faceplate with traditional clock art, and a Latin inscription on the drive cog for the hours ring that translates roughly to “Time rules all.” When we looked that up we found that “tempus rerum imperator” is the motto of the Worshipful Company of Clockmakers, the very existence of which we find pleasing in the extreme.
The clock runs through its initialization routine in the brief video below. We’re not sure we’d want this on our nightstand, but it’s certainly a unique and enjoyable way to show the passage of time. It sort of reminds us of this three-ringed perpetual calendar, but just a bit more stochastic.
Continue reading “This Classy But Chaotic Gear Clock Keeps You Guessing”
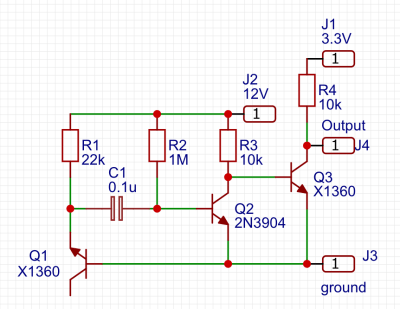One of the simplest circuits for generating random analogue noise involves a reverse biased diode in either Zener or avalanche breakdown, and it is a variation on this that he’s using. A reverse biased emitter junction of a transistor produces noise which is amplified by another transistor and then converted to a digital on-off stream of ones and zeroes by a third. Instead of a shift register to create his four bits he’s using four identical circuits, with no clock their outputs randomly change state at will.
